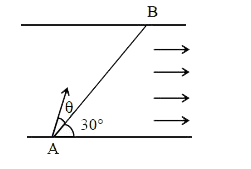
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A swimmer wants to cross a river from point A to point B. Line AB make...
Text Solution
|
- A river is flowing with a speed of 1 km h^-1 A swimmer wants to go poi...
Text Solution
|
- A swimmer crosses the river along the line making an angle of 45^@ wit...
Text Solution
|
- Two swimmers A and B start swimming from different positions on the sa...
Text Solution
|
- A swimmer wands to cross a river and reach point B directly from A. Th...
Text Solution
|
- A swimmer starts to swim from point a to cross a river. He wants to re...
Text Solution
|
- A river is flowing with a speed of 1 km/hr. A swimmer wants to go to p...
Text Solution
|
- A swimmer starts to swim from point a to cross a river. He wants to re...
Text Solution
|
- A swimmer crosses the river along the line making an angle of 45^(@) w...
Text Solution
|