Topper's Solved these Questions
TRIANGLES
MTG IIT JEE FOUNDATION|Exercise EXERCISE (Multiple Choice Questions) (LEVEL-1 )|35 VideosTRIANGLES
MTG IIT JEE FOUNDATION|Exercise EXERCISE (Multiple Choice Questions) (LEVEL-2 )|10 VideosTRIANGLES
MTG IIT JEE FOUNDATION|Exercise NCERT SECTION (Exercise 7.4)|6 VideosSTATISTICS
MTG IIT JEE FOUNDATION|Exercise Olympiad/HOTS Corner |20 Videos
Similar Questions
Explore conceptually related problems
MTG IIT JEE FOUNDATION-TRIANGLES-NCERT SECTION (Exercise 7.5)
- ABC is a triangle. Locate a point in the interior of DeltaABC which is...
Text Solution
|
- In a triangle, locate a point in its interior which is equidistant fro...
Text Solution
|
- In a huge park, people are concentrated at three points (see figure): ...
Text Solution
|
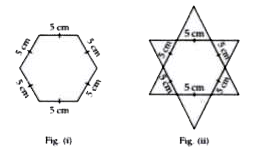
- Complete the hexagonal and star shaped Rangolies (see fig. (i) and (ii...
Text Solution
|