Home
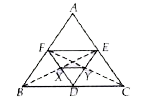
Class 9
MATHS
In the given figure, D, E and F are the ...

In the given figure, D, E and F are the midpoints of the sides BC, CA and AB of `DeltaABC. BE` bisect DF at X while CF bisect DE at Y, then BC = a XY. Find a.

A

3

B

4

C

2

D

`1//4`

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • QUADRILATERALS

    MTG IIT JEE FOUNDATION|Exercise EXERCISE (Subjective Problems) (Very Short Answer Type)|10 Videos

  • QUADRILATERALS

    MTG IIT JEE FOUNDATION|Exercise EXERCISE (Subjective Problems) (Short Answer Type)|5 Videos

  • QUADRILATERALS

    MTG IIT JEE FOUNDATION|Exercise EXERCISE (Comprehension Type PASSAGE-II )|3 Videos

  • PROBABILITY

    MTG IIT JEE FOUNDATION|Exercise OLYMPIAD/HOTS CORNER|20 Videos

  • STATISTICS

    MTG IIT JEE FOUNDATION|Exercise Olympiad/HOTS Corner |20 Videos

Similar Questions

Explore conceptually related problems

If D,E and F be the middle points of the sides BC,CA and AB of the Delta ABC, then AD+BE+CF is

In a triangle ABC, D, E and F are the mid-points of the sides BC, CA and AB, respectively. BE and DF intersect at X. DE and CF intersect at Y. Find XY = ? A) (1)/(2) BC B) (1)/(4) BC C) (1)/(3) BC D) (2)/(3) BC

In the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral DeltaABC. Prove that DeltaDEF is also an equilateral triangle.

Points D, E and F are the midpoints of sides AB, BC, and AC of DeltaABC . If DE = 10 cm, EF = 12 cm and DF = 8 cm, then find AB.

D, E and F are respectively the mid-points of the sides BC, CA and AB of a DeltaABC . Show that ar(triangleDEF)=1/4ar(triangleABC)

D, E and F are respectively the mid-points of the sides BC, CA and AB of a DeltaABC . Show that ar(BDEF) = 1/2ar(triangleABC)

if D,E and F are the mid-points of the sides BC,CA and AB respectively of the DeltaABC and O be any points, then prove that OA+OB+OC=OD+OE+OF