Topper's Solved these Questions
AREAS OF PARALLELOGRAMS AND TRIANGLES
MTG IIT JEE FOUNDATION|Exercise NCERT SECTION ( EXERCISE 9.1)|1 VideosAREAS OF PARALLELOGRAMS AND TRIANGLES
MTG IIT JEE FOUNDATION|Exercise NCERT SECTION ( EXERCISE 9.2)|7 VideosAREAS OF PARALLELOGRAMS AND TRIANGLES
MTG IIT JEE FOUNDATION|Exercise Olympiad/HOTS Corner |14 VideosCIRCLES
MTG IIT JEE FOUNDATION|Exercise OLYMPIAD/HOTS CORNER |6 Videos
Similar Questions
Explore conceptually related problems
MTG IIT JEE FOUNDATION-AREAS OF PARALLELOGRAMS AND TRIANGLES-SOLVED EXAMPLES
- Which of the following figures lie on the same base and between the sa...
Text Solution
|
- Compute the area of quadrilateral ABCD.
Text Solution
|
- In the given figure angleAOB= 90°, AC= BC, OA = 12 cm and OC = 6.5 cm....
Text Solution
|
- PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 c...
Text Solution
|
- P is any point on the diagonal BD of the parallelogram ABCD. Prove tha...
Text Solution
|
- ABCD is a quadrilateral. The straight line through C parallel to the d...
Text Solution
|
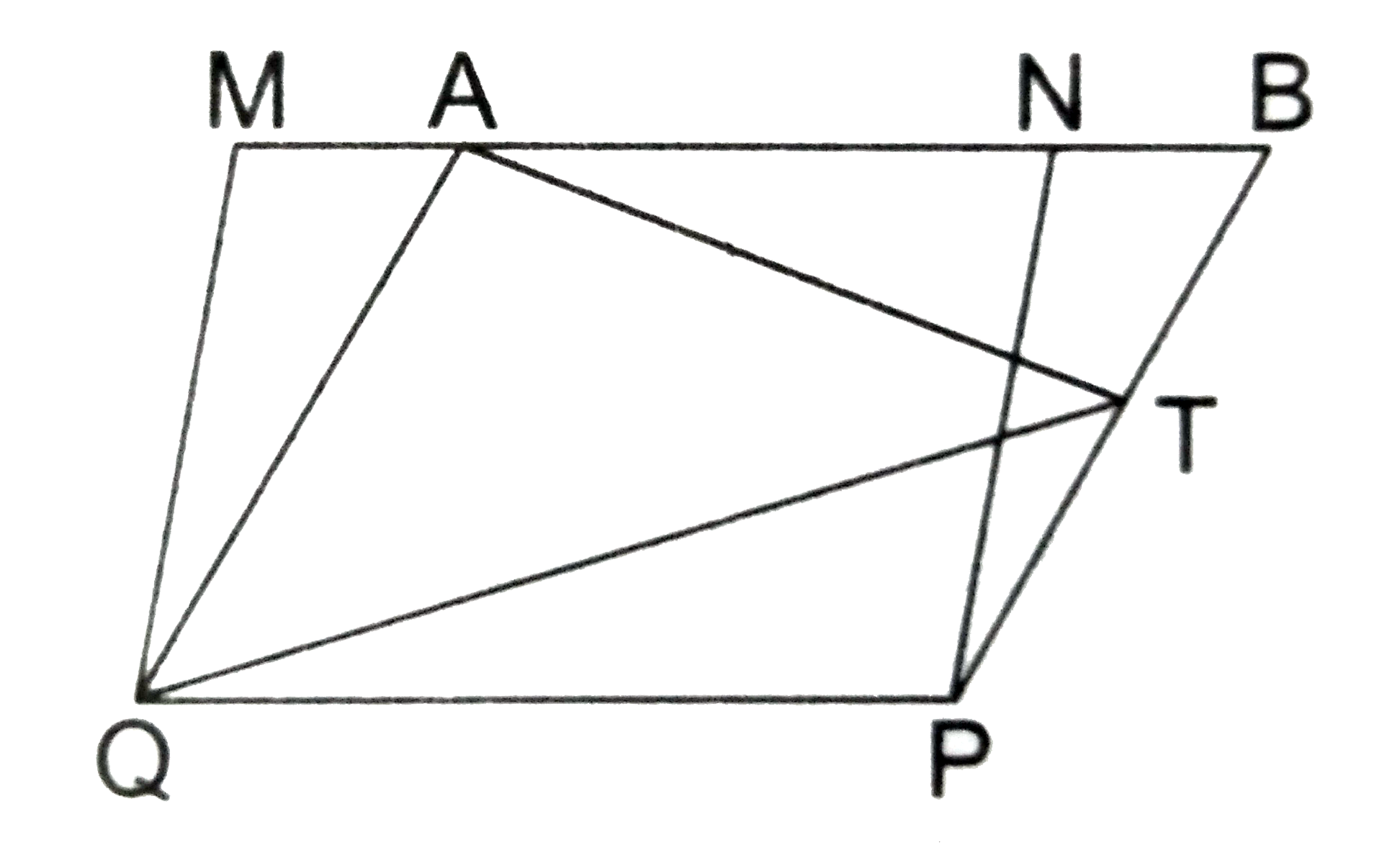
- In the adjoining figure, MNPQ and ABPQ are parallelogram and T is any ...
Text Solution
|
- In Figure, O C D E is a rectangle inscribed in a quadrant of a circ...
Text Solution
|
- If the diagonals A C ,\ B D of a quadrilateral A B C D , interse...
Text Solution
|
- Show that the area of a rhombus is half the product of the lengths ...
Text Solution
|
- A point D is taken on the side BC of a DeltaABC such that BD = 2DC. Pr...
Text Solution
|
- In the given figure, BC||XY, BX||CA and AB ||YC. Prove that area (Delt...
Text Solution
|
- In the given figure PSDA is a parallelogram in which PQ =QR= RS and A...
Text Solution
|
- ABC is a triangle in which D is the midpoint of BC and E is the midpo...
Text Solution
|