Home
Class 9
MATHS
Find the area of the given triangle....

Find the area of the given triangle.

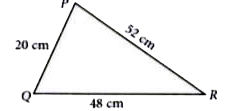
Text Solution

Verified by Experts

The correct Answer is:
`480 cm^2`
Promotional Banner

Topper's Solved these Questions

  • FOOTSTEPS TOWARDS CBSE BOARD

    MTG IIT JEE FOUNDATION|Exercise PART-B (SECTION-IV)|4 Videos

  • FOOTSTEPS TOWARDS CBSE BOARD

    MTG IIT JEE FOUNDATION|Exercise PART-A (SECTION-II)|16 Videos

  • FOOTSTEPS TOWARDS (JEE MAIN)

    MTG IIT JEE FOUNDATION|Exercise Section B (Numerical Value Type Questions)|10 Videos

  • HERON'S FORMULA

    MTG IIT JEE FOUNDATION|Exercise OLYMPIAD/HOTS CORNER|7 Videos

Similar Questions

Explore conceptually related problems

The sides of a triangle are 21, 20 and 13 cm. Find the area of the larger triangle into which the given triangle is divided by the perpendicular upon the longest side from the opposite vertex.

Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,-1),(2,1)and (0,3). Find the ratio of this area to the area of the given triangle.

Find the area of the triangle formed by joining the mid-points of the sides of the triangle, whose vertices are (2, - 4), (6, 2) and (- 4, 6). Find the ratio of this area to the area of the given triangle.

Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0,1),(2,1) and (0,3). Find the ratio of this area to the area of the given triangle.

If the two legs of a right-angled triangle are 3cm" and "4cm ,find the area of the triangle. Find the length of the base of a triangle

Corresponding sides of two similar triangles are in the ratio 1:3. If the area of the smaller triangle in 40cm^(2), find the area of the larger triangle.

The corresonding sides of two similar triangle are in the ratio 2:3 . If the area of the smaller trianle is 48 cm^(2) , find the area of the larger triangle.

Let be the area of a triangle.Find the area of a triangle whose each side is twice the side of the given triangle.

Vertices Ba n dC of A B C lie along the line (x+2)/2=(y-1)/1=(z-0)/4 . Find the area of the triangle given that A has coordinates (1,-1,2) and line segment B C has length 5.

Find the area of the triangle whose vertices are given below (-3,-4), (-2,-7), (-1,-9)