Home
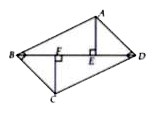
Class 7
MATHS
CF and AE are equal perpendiculars on BD...

CF and AE are equal perpendiculars on BD, BF = FE = ED

ABCD is a

A

Rectangle

B

Square

C

Rhombus

D

Kite

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • CONGRUENCE OF TRIANGLES

    MTG IIT JEE FOUNDATION|Exercise Subjective Problems (Very Short Answer Type)|10 Videos

  • CONGRUENCE OF TRIANGLES

    MTG IIT JEE FOUNDATION|Exercise Subjective Problems (Short Answer Type)|12 Videos

  • CONGRUENCE OF TRIANGLES

    MTG IIT JEE FOUNDATION|Exercise Assertion & Reaction Type|5 Videos

  • COMPARING QUANTITIES

    MTG IIT JEE FOUNDATION|Exercise Olympaid/HOTS Corner|20 Videos

  • DATA HANDLING

    MTG IIT JEE FOUNDATION|Exercise Olympiad / Hots Corner |20 Videos

Similar Questions

Explore conceptually related problems

CF and AE are equal perpendiculars on BD, BF = FE = ED DeltaABE is congruent to

CF and AE are equal perpendiculars on BD, BF = FE = ED angleBAE= ____.

Consider the following statements : 1. If the diagonals of a parallelogram ABCD are perpendicular , then ABCD may be a rhombus. 2. If the diagonals of a quadrilateral ABCD are equal and perpendicular , then ABCD is a square. Which of the statements given above is/are correct ?

Diagonals of a parallelogram ABCD intersect at Odot AL and CM are perpendiculars to BD such that L and M lie on BD .IS AL=CM? why or why not?

In quadrilateral ABCD, BM and DN are drawn perpendicular to AC such that BM = DN. If BR = 8 cm, then BD is

ABCD is a Parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB= 10cm, AE = 8cm, CF =12cm . Find AD ?

In the given figure, AB is a diameter of a circle and CD is perpendicular to AB, if AB = 10 cm and AE = 2 cm, then what is the length of ED ?

In a quadrilateral ABCD, it is given that AB ||CD and the diagonals AC and BD are perpendicular to each other. Show that AD.BC >= AB. CD.

In the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that : (i) DeltaADN =DeltaCBP (ii) AN=CP