Home
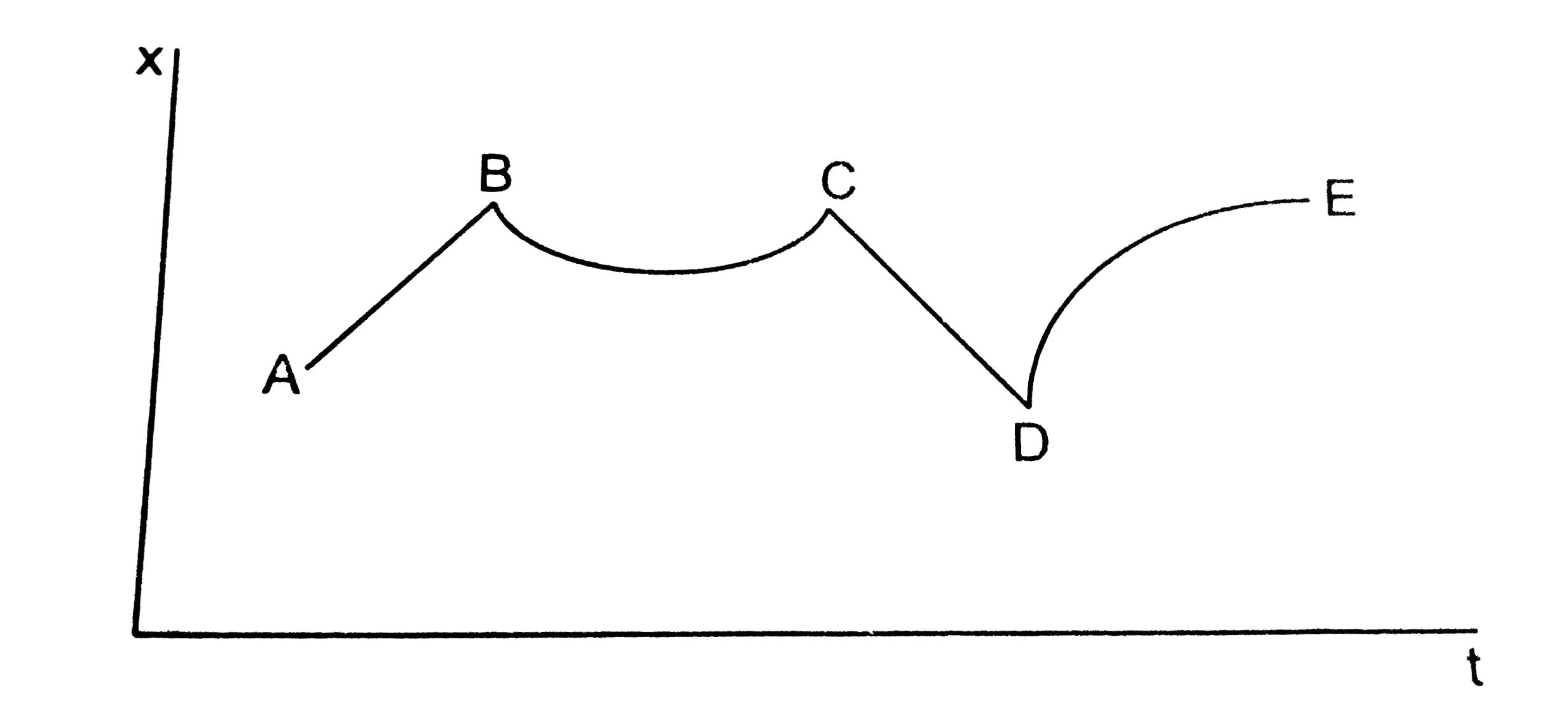
Class 9
PHYSICS
Figure shows the displacement of a parti...

Figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

A

AB

B

BC

C

CD

D

DE

Text Solution

Verified by Experts

The correct Answer is:
A
In the region AB, the displacement - time graph is a straight line whereas in all other regions it is curved. Thus, acceleration is zero in the region AB whereas it is non-zero in all other regions
According to Newton.s second law of motion, the force acting on the particle is F = ma
where m is the mass of the particle and a is its acceleration
for region AB = a = 0
`:. F = 0 `
Thus, the force acting on the particle is zero is region AB
Promotional Banner

Topper's Solved these Questions

  • FOOTSTEPS TOWARDS JEE MAIN

    MTG IIT JEE FOUNDATION|Exercise Section B (Numerical Value Type Questions)|10 Videos

  • FOOTSTEPS TOWARDS CBSE BOARD

    MTG IIT JEE FOUNDATION|Exercise Section - D |14 Videos

Similar Questions

Explore conceptually related problems

Figure shows the displacement time graph of a particle moving on the X-axis

Figure shows the position of a particle moving on the X-axis as a function of time.

Figure shows the position of a particle moving on the x - axis as a function of time

Figure show the displacement - time graph of a particle moving on the x-axis

Figure shows the position of a particle moving on the x-axis as a function of time, Choose the WRONG statement.

Figure shows the displacement (x)-time (f) graph of a particle moving on the X-axis.

The displacement time curve of a particle is shown in the figure. The external force acting on the particle is :

The displacement of a particle moving along x-axis is given by : x = a + bt + ct^2 The acceleration of the particle is.

Figure shows the graph of the x-coordinaste of a particle going along the X-axis as a function of time.Find a. te average velocity during 0 to 10s, b. instantaneous velocity at 2,5,8 and 12s.

The displacement of a particle along the x- axis it given by x = a sin^(2) omega t The motion of the particle corresponds to