Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SAMPLE QUESTION PAPER-X (UNSOLVED)
ACCURATE PUBLICATION|Exercise SECTION-B|8 VideosSAMPLE QUESTION PAPER-X (UNSOLVED)
ACCURATE PUBLICATION|Exercise SECTION-C|8 VideosSAMPLE QUESTION PAPER-X (UNSOLVED)
ACCURATE PUBLICATION|Exercise SECTION-A (FILL IN THE BLANKS)|8 VideosSAMPLE QUESTION PAPER-VIII
ACCURATE PUBLICATION|Exercise SECTION-D|6 VideosSAMPLE QUESTIONS PAPER - III (UNSOLVED)
ACCURATE PUBLICATION|Exercise SECTION - D|6 Videos
Similar Questions
Explore conceptually related problems
ACCURATE PUBLICATION-SAMPLE QUESTION PAPER-X (UNSOLVED)-SECTION-A (TRUE OR FALSE)
- tan^(-1) sqrt(x) = (1)/(2) cos^(-1) ((1-x)/(1+x)), x in [0, 1]
Text Solution
|
- If A= [(3,1),(7,5)], then A^(-1)= (1)/(8)[(5,-1),(-7,3)]
Text Solution
|
- If x= a cos^(3) theta, y= b sin^(3) theta, " then "(dy)/(dx)= (b)/(a) ...
Text Solution
|
- prove int(dx)/(sqrt(x^2-a^2)) = log|x+sqrt(x^2-a^2)|+c
Text Solution
|
- If veca" and "vecb are any two vectors, then (veca xx vecb)^(2)= |veca...
Text Solution
|
- If the points (-1, 3, 2), (-4, 2, -2)" and "(5, 5, lambda) are colline...
Text Solution
|
- The probability that A will solve a problem is (2)/(3) and B will solv...
Text Solution
|
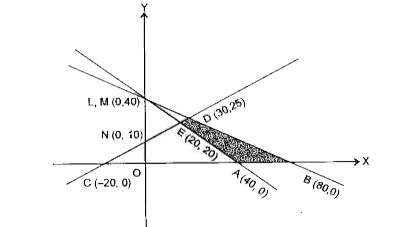
- The corner points of the function Z= 3x+4y" are "(40, 0), (80, 0), (30...
Text Solution
|