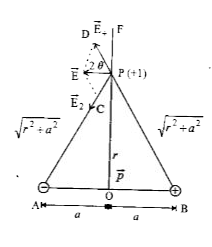
Consider an electric dipole AB of length 2a. Let P be the point on the equatorial line at a distance r from the centre of the dipole.
Electric field intensity at P due to +q carge is given by
`vecE_(1)=1/(4 pi varepsilon_(0))q/(BP^(2))"along PD"`
`vecE_(1)=1/(4 pi varepsilon_(0))q/((sqrt(r^(2)+a^(2)))^(2))"along PD"`
`vecE_(1)=1/(4 pi varepsilon_(0))q/(r^(2)+a^(2))"along PD"`
Electric field intensity at P due to `-q` given by
`vecE._(2)=1/(4 pi varepsilon_(0))q/(AP^(2))"along PC"`
`vecE._(2)=1/(4 pi varepsilon_(0))q/((sqrt(r^(2)+a^(2)))^(2))"along PC"`
`:." "abs(vecE_(1))=abs(vecE_(2))=1/(4 pi varepsilon_(0))q/((r^(2)+a^(2)))`
`vecE_(1) and vecE_(2)`, are inclined at an angle of 2`theta`. So, using parallelogram law, the net electric field intensity can be measured.
`:." "sqrt(E_(1)^(2)+E_(2)^(2)+2E_(1)E_(2) cos2theta)`
`=sqrt(E_(1)^(2)+E_(1)^(2)+2E_(1)^(2) cos 2 theta)" "[:. E_(1)=E_(2)]`
`=sqrt(2E_(1)^(2)+2E_(1)^(2)cos 2 theta)`
`sqrt(2E_(1)^(2)(1+cos 2 theta))`
`=sqrt(2E_(1)^(2) xx 2 cos^(2)theta)" "[:.(1+cos 2 theta= 2 cos^(2)theta)]`
`E=2 E_(1) cos theta`
`:." "E = 2 xx 1/(4 pi varepsilon)q/(r^(2)+a^(2))cos theta" "...(1)`
Now from `Delat" "OAP`
`cos theta=a/(sqrt(r^(2)+a^(2)))`
From equation (1)
`:." "E=2 xx 1/(4 pi varepsilon_(0))q/(r^(2)+a^(2)) xx a/(sqrt(r^(2)+a^(2)))`
`E=(q xx2a)/(4 pi varepsilon_(0)(r^(2)+a^(2))^(3//2))`
Now`" "q xx 2a =p" "("dipole moment")`
`E=p/(4 pi varepsilon_(0)(r^(2)+a^(2))^(3//2))"along(-a)axis"" "...(2)`
In vector form
`vecE=(-vecp)/(4 pi varepsilon_(0)(r^(2)+a^(2))^(3//2))`
The direction of electric field `vecE` is opposite to the direction of the dipole moment of electric dipole.
We know that
For an ideal dipole a << `:." "a^(2) "can be neglected as compared to" r^(2)`.
`:." "`from eq. (2)
`E=p/(4 pi varepsilon_(0)(cancel(r^(2)))^(3//cancel2))`
`E=p/(4 pi varepsilon_(0)r^(3))"along"(-)"x-axis"`
`:." "Eprop 1/r^(3)`