Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SYMMETRY
NAND LAL PUBLICATION|Exercise EXERCISE 14.1 |10 VideosSYMMETRY
NAND LAL PUBLICATION|Exercise EXERCISE 14.2|2 VideosSIMPLE EQUATIONS
NAND LAL PUBLICATION|Exercise SAMPLE PAPER FOR PRACTICE|23 VideosTHE TRIANGLE AND ITS PROPERTIES
NAND LAL PUBLICATION|Exercise Sample Paper for Practice |9 Videos
Similar Questions
Explore conceptually related problems
NAND LAL PUBLICATION-SYMMETRY -SAMPLE PAPER FOR PRACTICE (Answer the following :)
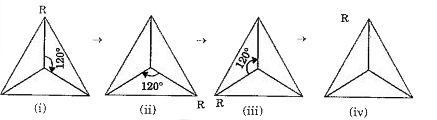
- (a) Can you now tell the order of the rotational symmetry for an equil...
Text Solution
|
- What is the other name for lines of symmetry for (i) Isosceles tria...
Text Solution
|
- Name any two figures that have both line symmetry and rotational symme...
Text Solution
|
- Name the two gemetrical shapes which have line of symmetry and no rota...
Text Solution
|
- Name the two geometrical shapes which have no line of symmetry nor rot...
Text Solution
|
- Name a shape which has rotational symmetry but not line of symmetry.
Text Solution
|
- Find the order of rotational symmetry for the angle of rotation 60^(@)...
Text Solution
|
- At what angle will the fan blades show rotational symmetry, if the num...
Text Solution
|
- How can you say that the figure possesses rotational symmetry of order...
Text Solution
|
- Draw two alphabets which show line of symmetry but no rotational symme...
Text Solution
|