Home
Class 8
MATHS
Find the area of these quadrilaterals....

Find the area of these quadrilaterals.

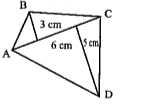
Text Solution

Verified by Experts

The correct Answer is:
24`cm^2`
Promotional Banner

Topper's Solved these Questions

  • MENSURATION

    NAND LAL PUBLICATION|Exercise DO THIS|10 Videos

  • MENSURATION

    NAND LAL PUBLICATION|Exercise THINK DISCUSS AND WRITE|9 Videos

  • MENSURATION

    NAND LAL PUBLICATION|Exercise SAMPLE PAPER FOR PRACTICE|19 Videos

  • LINEAR EQUATIONS IN ONE VARIABLE

    NAND LAL PUBLICATION|Exercise SAMPLE PAPER FOR PRACTICE |21 Videos

  • PRACTICAL GEOMETRY

    NAND LAL PUBLICATION|Exercise SAMPLE PAPER FOR PRACTICE|15 Videos

Similar Questions

Explore conceptually related problems

The vertices of a quadrilateral are situated at foci and the extremities of the minor axis of the ellipse 4x^2+9y^2=36 . Find the area of the quadrilateral.

A diagonal of a quadrilateral is 28.4 m long.The perpendiculars to the diagonal from opposite vertices are of lengths 7.20 m and 8.80 m.Find the area of the quadrilateral.

Find the area of the quadrilateral ABCD in which AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angleABC = 90^@

Find the area of the quadrilateral ABCD in which AD = 24 cm, angleBAD = 90^@ and BCD forms an equilateral triangle whose each side is 26 cm.

Find the area of the quadrilateral ABCD Here, AC = 22 cm, BM = 3 cm, DN = 3 cm , and BM botAC, DN bot AC

Find the area of the quadrilateral whose vertices taken in order, are (-4, - 2), (-3,-5), (3, -2),(2,3).

From a point A, common tangents are drawn to the circle x^2+y^2=a^2/2 and parabola y^2= 4x . Find the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola.

If A(-5, 7), B(- 4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD,

Let A be the centre of the circle x^2+y^2-2x-4y-20=0 . If the tangents at the points B (1, 7) and D(4,-1) on the circle meet at the point C find the area of the quadrilateral ABCD.