A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
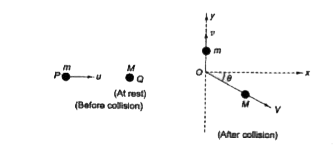
- A body P of mass m moving along the positive x-direction with velocity...
Text Solution
|
- A body of mass m moving with a velocity v in the x direction collides ...
Text Solution
|
- A body of mass 'm' moving with certain velocity collides with another ...
Text Solution
|
- A body of mass m is at rest. Another body of same mass moving with vel...
Text Solution
|
- A body of mass M moving with a speed u has a ‘head on’, perfectly elas...
Text Solution
|
- A body of mass m moving with velocity V along the X-axis, collides wit...
Text Solution
|
- A body of mass m is moving along x-axis with a velocity V, and another...
Text Solution
|
- A body of mass m is moving along x-axis with a velocity V, and another...
Text Solution
|
- A body of mass 1 kg makes an elastic collision with another body at r...
Text Solution
|