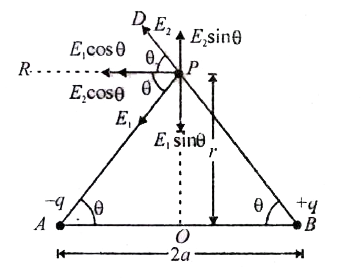
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Derive an expression for-electric field intensity at any point on equa...
Text Solution
|
- (a) Derive and expression for the electric field at any point on the e...
Text Solution
|
- Derive an expression for the intensity of the electric field at a poin...
Text Solution
|
- Two point charges +4q and +q are placed 30 cm apart. The electric fiel...
Text Solution
|
- Two point charges +Q and -Q are separated by a certain distance. The r...
Text Solution
|
- Two point charges q and-q are placed at a distance 2a part. Calculate ...
Text Solution
|
- Two point charges q and -q is placed at a distance 2a apart.Calculate ...
Text Solution
|
- Two point charges +Q and -Q are separated by a certain distance. The r...
Text Solution
|
- Derive the expression for the electric field intensity due to an elect...
Text Solution
|