Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAND LAL PUBLICATION-TRIANGLES -EXERCISE 6.3
- State which pairs of triangles in Fig. are similar. Write the similari...
Text Solution
|
- State which pairs of triangles in Fig. are similar. Write the similari...
Text Solution
|
- State which pairs of triangles in Fig. are similar. Write the similari...
Text Solution
|
- In fig., triangleODC-triangleOBA, angleBOC=125@0 and angleCDO=70@0. F...
Text Solution
|
- Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each o...
Text Solution
|
- In fig., (QR)/(QS)=(QT)/(PR) and angle1=angle2 . Show that trianglePQS...
Text Solution
|
- D is a point on side BC of Delta ABC such that AD = AC (see Fig. 7.47)...
Text Solution
|
- In figure triangleABE=triangleACD show that triangleADE~triangleABC . ...
Text Solution
|
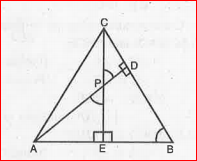
- In figure, altitudes AD and CE of DeltaABC intersect each ther at the ...
Text Solution
|
- In figure, altitudes AD and CE of DeltaABC intersect each ther at the ...
Text Solution
|
- In Fig., altitudes AD and CE of triangleABC intersect each other at th...
Text Solution
|
- In Fig., altitudes AD and CE of triangleABC intersect each other at th...
Text Solution
|
- DeltaABC and DeltaDBC are two isosceles triangles on the same base BC ...
Text Solution
|
- In Fig., ABC and AMP are two right triangles, right angled at B and M ...
Text Solution
|
- In Fig., ABC and AMP are two right triangles, right angled at B and M ...
Text Solution
|
- CD and GH are respectively the bisectors of angleACB and angleEGF such...
Text Solution
|
- CD and GH are respectively the bisectors of angleACB and angleEGF such...
Text Solution
|
- CD and GH are respectively the bisectors of angleACB and angleEGF such...
Text Solution
|
- In Fig., E is a point on side CB produced of an isosceles triangle ABC...
Text Solution
|
- If AD and PM are medians of triangles ABC and PQR, respectively where...
Text Solution
|
 .
.