Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAND LAL PUBLICATION-TRIANGLES -EXERCISE 6.6
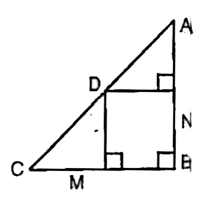
- In figure , D is point on hypotenuse AC of Delta ABC , BD bot AC, DM ...
Text Solution
|
- In figure , D is point on hypotenuse AC of Delta ABC , BD bot AC, DM ...
Text Solution
|
- In figure, ABC is a triangle in which angle ABC gt 90^(@) and AD bot C...
Text Solution
|
- In figure, AD is a median of a triangle ABC and AM bot BC. Prove that ...
Text Solution
|
- In figure, AD is a median of a triangle ABC and AM bot BC. Prove that ...
Text Solution
|
- In figure, AD is a median of a triangle ABC and AM bot BC. Prove that ...
Text Solution
|
- Prove that sum of squares of the diagonals of a parallelogram is equal...
Text Solution
|
- In two chords AB and CD intersect each AB and CD intersect each other ...
Text Solution
|
- In two chords AB and CD intersect each AB and CD intersect each other ...
Text Solution
|
- In two chords AB and CD of a circle intersect each other at the point ...
Text Solution
|
- In two chords AB and CD of a circle intersect each other at the point ...
Text Solution
|