A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DISHA PUBLICATION-MENSURATION-TEST YOURSELF
- PQRS is a square. SR is a tangent (at point S) to the circle with cent...
Text Solution
|
- In the diagram, all triangles are equilateral. If AB = 16, then the to...
Text Solution
|
- The length and breadth of the floor of the room are 20 feet and 10 ...
Text Solution
|
- O is the centre of a circle of radius 5 cm. The chord AB subtends an a...
Text Solution
|
- The length, breadth and height of a cuboid are in the ratio 1:2:3. The...
Text Solution
|
- A boat having a length of 3 m and breadth of 2 m is floating on a lake...
Text Solution
|
- An icecream company makes a popular brand of icecream in a rectangular...
Text Solution
|
- A hemispherical bowl is filled to the brim with a beverage. The con...
Text Solution
|
- If the curved surface area of a cone is thrice that of another cone an...
Text Solution
|
- The minute hand of a clock is 10 cm long. Find the area of the face...
Text Solution
|
- Find the length of the string wound on a cylinder of height 48 cm and ...
Text Solution
|
- Iron weights 8 times the weight of oak. Find the diameter of an iron b...
Text Solution
|
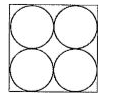
- Four identical coins are placed in a square. For each coin, the ratio ...
Text Solution
|
- A punching machine is used to punch a circular hole of diameter two un...
Text Solution
|
- A punching machine is used to punch a circular hole of diameter two un...
Text Solution
|