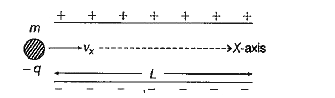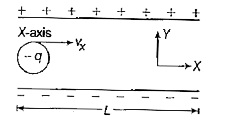Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the above diagram, a particle of mass m and charge (- q) initially ...
Text Solution
|
- A paraticale of mass m and charge (-q) enters the region between the ...
Text Solution
|
- Between two horizontal parallel plates, uniform electric field E direc...
Text Solution
|
- प्रारम्भ में, x-अक्ष के अनुदिश v(x) चाल से गति करती हुए दो आवेशित प्ले...
Text Solution
|
- A particle of mass m and charge (-q) enters the region between the two...
Text Solution
|
- द्रव्यमान m तथा आवेश (-q) का एक कण x-अक्ष के अनुदिश v चाल से गतिशील है...
Text Solution
|
- A particle of mass m and charge(-q) enters the region between the ...
Text Solution
|
- A uniform electric field of magnitude E exists in between two parallel...
Text Solution
|
- A uniform electric field vecE exists between the plates of a charged c...
Text Solution
|