Magnetic field along the axis of a circular current carrying loop Consider a circular loop of wire of radius a and carrying current I as shown in the figure. Let the plane of the loop be perpendicular to the plane of paper. We wish to find field B at an axial point P at a distance r from the centre C.
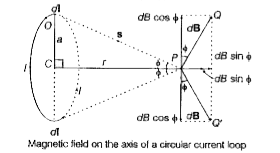
Magnetic field on the axis of a circular current loop
Consider a current element d I at the top of the loop. It has an outward coming current.
If s be the position vector of point P relative to the element d I, then from Biot-Savart law, the field at point P due to the current element is
`dB=(mu_(0))/(4pi) *(Idl sin theta)/(s^(2))`
Since, `d I bot s`, i.e. `theta=90^(@)`, therefore
`dB=(mu_(0))/(4pi)*(Idl)/(s^(2))`
The field dB lies in the plane of paper and is perpendicular to s, as shown by PQ. Let `phi` be the angle between OP and CP. Then, dB can be resolved into two rectangular components.
(a) dB sin o along the axis,
(b) dB cos o perpendicular to the axis.
For any two diametrically opposite elements of the loop, the components perpendicular to the axis of the loop will be equal and opposite and will cancel out. Their axial components will be in the same direction, i.e. along CP and get added up.
`:.` Total magnetic field at the point P in the direction CP is
`B= intdB sin phi`
But `sin phi =(a)/(s) and dB=(mu_(0))/(4pi) *(Idl)/(s^(2))`
`:. B= int (mu_(0))/(4pi) *(Idl)/(s^(2)) *(a)/(s)`
Since, `mu_(0)` and I are constant, and s and a are same for all points on the circular loop, we have
`B=(mu_(0)Ia)/(4pis^(3))int dl=(mu_(0)Ia)/(4pis^(3))*2pia`
`[ :. int dl="circumference"=2pia]`
`=(mu_(0)Ia^(2))/(2s^(3))`
Now, `s=(r^(2)+a^(2))^(1//2)`
`:. B=(mu_(0) Ia^(2))/(2(r^(2)+a^(2))^(3//2))`
If the coil consists of turns, then
`B=(mu_(0)NIa^(2))/(2(r^(2)+a^(2))^(3//2))`
At the centre of the current carrying loop r = 0,
therefore
`B=(mu_(0)NIa^(2))/(2a^(3)) =(mu_(0)NI)/(2a) or B=(mu_(0)NIA)/(2pi a^(3))`
