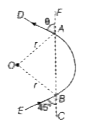
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m = 1.6 xx10^(-27) kg and charge q=1.6xx10^(-19)C e...
Text Solution
|
- A particle of mass m = 1.6 xx 10^(27) kg and charge q = 1.6 xx 10^(-19...
Text Solution
|
- A particle of mass m=1.6xx10^-27 kg and charge q=1.6xx10^-19C enters a...
Text Solution
|
- A particle of charge -q and mass m enters a uniform magnetic field vec...
Text Solution
|
- A particle having mass m , charge q enters a cylindrical region having...
Text Solution
|
- A particle of mass 1.6xx10^(-27) kg and charge 1.6 xx 10^(-19) coulomb...
Text Solution
|
- द्रव्यमान m=1.6 xx 10^(-27) किग्रा तथा आवेश q= 1.6x10^(-19) कूलॉम का ए...
Text Solution
|
- द्रव्यमान m व आवेश q का एक कण एक समान चुम्बकीय क्षेत्र में v वेग से क्...
Text Solution
|
- समरूप विद्युत क्षेत्र 1.6xx10^(5) Vm^(-1) में स्थित - कण का द्रव्यमान ...
Text Solution
|