Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
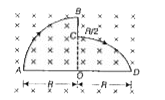
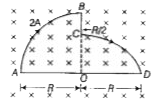
- Find the net force acting on the wire shown in the figure. [Take, B...
Text Solution
|
- The vessel shown in the figure contains water, take rho("water")=1000k...
Text Solution
|
- A wedge of mass M resting on a horizontal frictionless surface is acte...
Text Solution
|
- A small point mass m is placed at the centre of curvature of acircular...
Text Solution
|
- A lift is moving upwards as shown in figure in figure A block of mass ...
Text Solution
|
- In the circuit shown in figure resistance of each wire is r. Net resis...
Text Solution
|
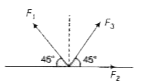
- Two forces act on a particle simultaneously as shown in the figure. F...
Text Solution
|
- There are four forces acting on a block as shown in the figure ,The ma...
Text Solution
|
- A force F acts on a particle kept on a rough surface as shown in the f...
Text Solution
|