Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
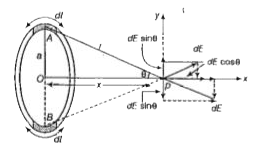
- A ring of radius a is charged and contains q charge uniformly distribu...
Text Solution
|
- A ring of radius a contains a charge q distributed uniformly over its ...
Text Solution
|
- Charges q is uniformly distributed over a thin half ring of radius R. ...
Text Solution
|
- A point charge q is located at the centre fo a thin ring of radius R w...
Text Solution
|
- त्रिज्या R के एक वलय पर आवेश q एकसमान रूप से वितरित है। इसकी अक्ष पर क...
Text Solution
|
- एक R त्रिज्या की पतली वलय पर Q आवेश एक समान रूप से वितरित है व...
Text Solution
|
- A charge is distributed uniformly over a ring of radius ‘a’. Obtain an...
Text Solution
|
- A charge Q is uniformly distributed over a ring of radius a.Obtain an ...
Text Solution
|
- Electric charge Q is uniformly distributed around a thin ring of radiu...
Text Solution
|