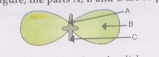
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In figure, the parts A,B and C are respectively:
Text Solution
|
- Figure-I-Mango, Figure-II-Coconut are shown in the following digram. I...
Text Solution
|
- The given figure indicates vertebral column of human (right lateral vi...
Text Solution
|
- In figure the parts A, B and C are sequentially
Text Solution
|
- Identify the labelled parts A,B and C in given figure:
Text Solution
|
- In the given figure of Cotyledon the parts labelled as A and B respect...
Text Solution
|
- In the given figure the parts A, B and C are sequentially area
Text Solution
|
- In the given figure of Cotyledon the parts labelled as A and B respect...
Text Solution
|
- In figure the parts A, B and C are sequentially
Text Solution
|