Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
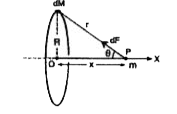
- A point of mass is at a distance x from the centre of a ring of mass M...
Text Solution
|
- Find the intensity of gravitational field at a point lying at a distan...
Text Solution
|
- A point mass m is a distance x from the centre of mass M and radius R ...
Text Solution
|
- Find the force of attraction on a particle of mass m placed at the cen...
Text Solution
|
- A ring of radius R is made from a thin wire of radius r. If rho is the...
Text Solution
|
- A solid sphere of mass m and radius r is placed inside a hollow thin s...
Text Solution
|
- A mass m is placed at point P lies on the axis of a ring of mass M and...
Text Solution
|
- Find potential at a point 'P' at a distance 'x' on the axis away from ...
Text Solution
|
- We know that when two equal masses are placed on a line then, gravitat...
Text Solution
|