A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
- A uniform sphere of mass M and radius R exerts a force F on a small ma...
Text Solution
|
- A particle of mass m is located outside a uniform sphere of mass M at ...
Text Solution
|
- The centres of a ring of mass m and a sphere of mass M of equal radius...
Text Solution
|
- From a solid sphere of mass M and radius R, a solid sphere of radius R...
Text Solution
|
- A uniform sphere has radius R. A sphere of diameter R is cut from its ...
Text Solution
|
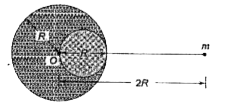
- There is a concentric hole of radius R in a solid sphere of radius 2R....
Text Solution
|
- find the gravitational force of attraction between a uniform sphere of...
Text Solution
|
- A solid sphere of mass M and radius R has a spherical cavity of radius...
Text Solution
|
- A particle of mass m is placed at a distance of 4R from the centre of ...
Text Solution
|