Home
Class 14
MATHS
DeltaABC and DeltaDBC have a common base...

`DeltaABC and DeltaDBC` have a common base and drawn towards one sides. `angleBAC = angleBDC = 90^(@)`. If AC and DB intersect at P, then:

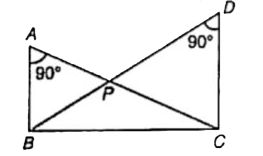
Text Solution

Verified by Experts

The correct Answer is:
`c^(2)gta^(2)+b^(2)`
Promotional Banner

Topper's Solved these Questions

  • CONGRUENCE AND SIMILAR TRIANGLES

    LUCENT PUBLICATION|Exercise EXERCISE-5A|47 Videos

  • CONGRUENCE AND SIMILAR TRIANGLES

    LUCENT PUBLICATION|Exercise EXERCISE-5B|8 Videos

  • CIRCLE AND ITS TANGENT LINES

    LUCENT PUBLICATION|Exercise EXERCISE 8B|27 Videos

  • ELEMENTARY TRIGONOMETRIC IDENTITIES

    LUCENT PUBLICATION|Exercise EXERCISE 11B|37 Videos

Similar Questions

Explore conceptually related problems

DeltaABC and DeltaDBC are on the same base BC but on opposite sides of it. AD and BC intersect each other at O. If AO=a cm, DO=b cm and the area of DeltaABC=x cm^(2) , then what is the area (in cm^(2) ) of DeltaDBC ?

Two triangles BACandBDC, right angled at Aand D respectively,are drawn on the same base BC and on the same side of BC. If AC and DB intersect at P, prove that APxPC=DPxPB.

In DeltaABC,angleB=90^(@). If P is the mid-point of side AC, then PA=PB=

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABD~=DeltaACD

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABP~=DeltaACP

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that AP bisects angleA as well as angleD .

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that : (i) DeltaABD cong DeltaACD (ii) DeltaABP cong DeltaACP (iii) AP bisects angleA as well as angleD (iv) AP is the perpendicular bisector of BC.

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that (i) DeltaABD ~=DeltaACD (ii) DeltaABE~=DeltaACE (iii) AE bisects angleA as well as angleD (iv) AE is the perpendicualr bisector of BC.

Slove the following questions. In the figure, DeltaADB and DeltaCDB are drawn on the same base BD.if AC and BD intersect at O, then prove that (A(DeltaADB))/(A(DeltaCDB)) = (AO)/(CO).