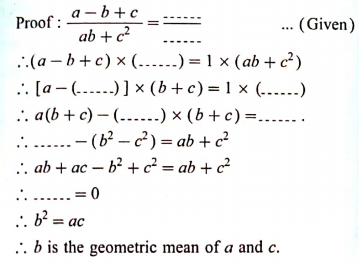Similar Questions
Explore conceptually related problems
Recommended Questions
- Fill in the blanks to prove that b is the geometric mean of a and c, i...
Text Solution
|
- Identify A, B. C and Din Figure 19.15 respectively. <img src="https:...
Text Solution
|
- In the given figure (not to scale), O is the centre of the circle. A,B...
Text Solution
|
- Which of the following are correct chain isomers of butane ? (i) <img ...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Dtermine the images of the following figure about the given line : ...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|