A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
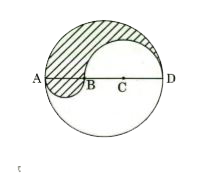
- In the figure given below, ABCD is the diameter of a circle of radius ...
Text Solution
|
- In the given figure (not to scale), O is the centre of the circle. A,B...
Text Solution
|
- In the figure above (not to scale), overline(AB)botoverline(CD) and AD...
Text Solution
|
- Find the area of the shaded region, given that the radius of each circ...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Find the area of figure given below.
Text Solution
|
- Find the perimeter of the figure given below.
Text Solution
|
- Find the area of the figure given below.
Text Solution
|
- In the figure given below, PQRS is a square of side 14 cm and two semi...
Text Solution
|