Home
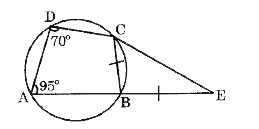
Class 14
MATHS
ABCD is a cyclic quadrilateral. The side...

ABCD is a cyclic quadrilateral. The side AB is extended to E in such a way that BE =BC. If `/_ADC = 70^@, /_BAD=95^@,` then `/_DCE` is equal to

A

`140^@`

B

`120^@`

C

`165^@`

D

`110^@`

Text Solution

Verified by Experts

The correct Answer is:
A

`/_DAB = 180^@ - 95^@`
` = 85^@`
`/_CBE = 70^@`
`Delta BCE` में, `BC = BE`
`implies /_BCE = /_BEC`
`therefore /_BCE = (180^@ - 70^@)/2 = 55^@`
`therefore /_BCE =85^@ + 55^@ = 140^@`
Promotional Banner

Similar Questions

Explore conceptually related problems

If ABCD is a cyclic quadrilateral, then cos A + cos B is equal to

In a cyclic quadrilateral ABCD, the side AB is extended to a point X. If /_XBC=82^(@) and /_ADB=47^(@) , then the value of /_BDC is

In the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If angle ADC=140^(@) , then find the value of angleBAC .

In Figure,ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A,B,C,D* If (/_ADC)=130^(0) find /_BAC

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle BAC= 50^@ . Then angle ADC is equal to: ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इसे घेरने वाले वृत्त का व्यास ह तथा कोण BAC= 50^@ है| कोण ADC का मान ज्ञात करें |

In the adjoining figure, ABCD is a cyclic quadrilateral.If side BC is produced upto point E and angleDAB=95^@ , then find the value of angleDCE .