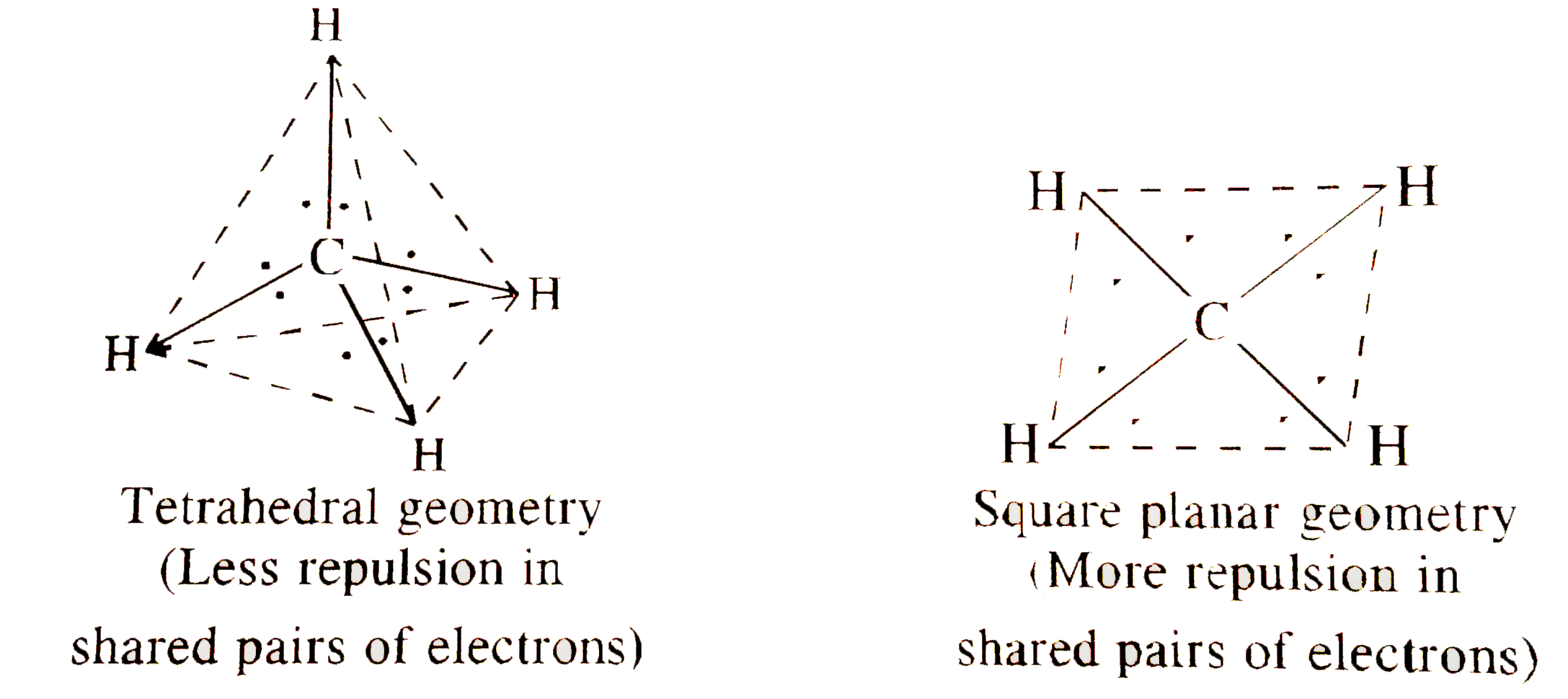Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Apart from tetrahedral geometry, another possible geometry for CH4 is ...
Text Solution
|
- Apart from tetrahedral geometry, another possible geometry for CH(4) i...
Text Solution
|
- Which has square planar geometry
Text Solution
|
- Apart from tetrahedral geometry, another possible geometry for CH(4) ...
Text Solution
|
- चतुष्फलकीय ज्यामिति के आलावा CH(4) अणु की एक और संभव ज्यामिति वर्ग-समत...
Text Solution
|
- Apart from tetrahedral geometry, another possible geometry for CH(4) i...
Text Solution
|
- The complex having square planar geometry is
Text Solution
|
- Apart from tetrahedral geometry, another possible geometry for CH(4) i...
Text Solution
|
- Apart from tetrahedral geometry, another possible geometry for CH(4) i...
Text Solution
|