Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
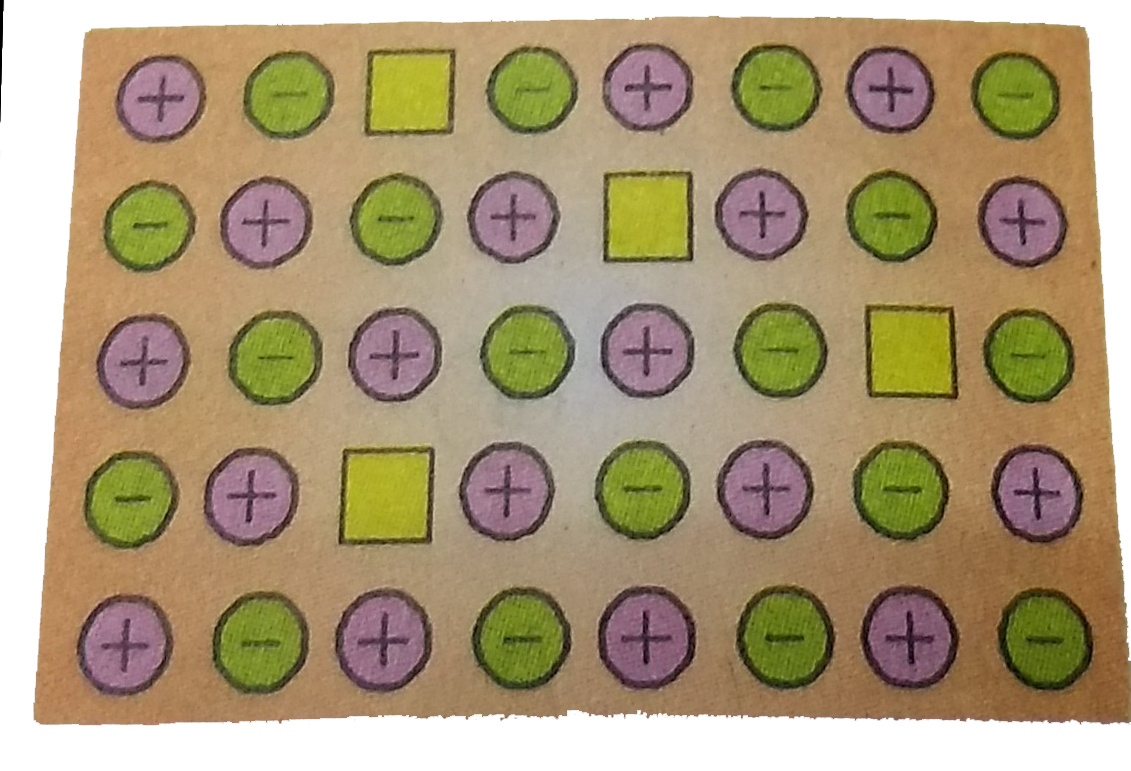
- Examine the illustration of a portion of the deffective crystal and an...
Text Solution
|
- Examine the illustration of a portion of the deffective crystal and an...
Text Solution
|
- Examine the given defective crystal : Answer the following questions :...
Text Solution
|
- Examiine the given defective crystal (i) What type of stoichiometric d...
Text Solution
|
- Examine the given defective crystal {:(A^(+), B^(-),A^(+),B^(-),A^(+))...
Text Solution
|
- Examine the given defective crystal {:(A^+, B^- , A^+ , B^- , A^+),(B^...
Text Solution
|
- What are vacancy and interstitial defects? How do these defects affect...
Text Solution
|
- Examine the illustration of a portion of the defective crystal given b...
Text Solution
|
- Examine the given defective crystal and {:(A^(+),B^(-),A^(+),B^(-),A^(...
Text Solution
|