Home
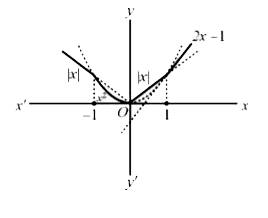
Class 12
MATHS
The number of points at which the functi...

The number of points at which the function,
`f (x)={{:(min {|x|"," x ^(2)}),(min (2x -1"," x^(2)}):}if x in (-oo,1)` otherwise is not differentiable is:

A

0

B

1

C

2

D

More than 2

Text Solution

Verified by Experts

The correct Answer is:
B
plotting graph of required function
zig-zag curve is the min. curve which is asked in the question
thus it appears that there are 2 pts. of non-differentiability
But at x=1 , L.H.D = 2x = 2 and R.H.D = 2
Thus there is only one pt. of non-differentiability
Promotional Banner

Similar Questions

Explore conceptually related problems

The number of critical points of the function f(x)=|x-1||x-2| is

The number of the points where the function f(x)=min_({|x|-1,|x-2|)|-1} is NOT derivable,is

The function f(x)=min{x-[x],-x-|-x|} is a

Find the number of critical points of the function f (x) = min (tan x , cos x) , x in (0 , pi)

Consider the function f(x)=min{|x^(2)-9|,|x^(2)-1|} , then the number of points where f(x) is non - differentiable is/are

Consider the function f(x)=min{|x^(2)-4|,|x^(2)-1|} , then the number of points where f(x) is non - differentiable is/are

The total number of points where the function f(x)=|x+2|+|x-1| is not differentiable is

If f(x)={min(x,x^(2)),x<=0 and min(2x,x^(2)-1),x<0 ,then find the number of non-differentiable points of f(x)

The function f(x) = min {|x|, sqrt(1-x^(2))}, -1lt x lt 1 possesses