Home
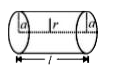
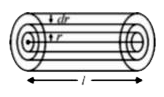
Class 12
PHYSICS
A solid cylindrical wire of length l has...

A solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as `rho=rho_(0)r`, where r is distance from axis of cylinder and `rho_(0)` is a positive constant quantity. The resistance across its ends is :

A

`(rho_(0)l)/(2pia)`

B

`(rho_(0)l)/(pia^(2))`

C

`(rho_(0)l)/(pia)`

D

`(2rho_(0)l)/(pi)`

Text Solution

Verified by Experts

The correct Answer is:
A
dR = Resistance of thin cylindrical shell of radius r and thickness (dr) `therefore dR =(rho l)/(2 pi r dr)`
Infinite number of thin cylinders are connected parallel to each other
`therefore (1)/(R )= int (1)/(dR)`
`rArr (1)/(R ) = int (2 pi r dr)/(rho l) =(2 pi)/(rho_(0)l) overset(a) underset(0) int (rdr)/(r)`
`rArr (1)/(R) =(2 pi a)/(rho 0l) therefore R =(rho 0 l)/(2 pi a)`
Promotional Banner

Similar Questions

Explore conceptually related problems

A conductor of length l and area of cross-section A has a resistance R then its specific resistance is

A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as rho = k//r^(2) where k is constant . The resistance of the cylinder is -

A cylindrical wire of length L and radius r has a resistance R. The resistance of another wire of the same material but half its length and half its radius will be:

A current i passes through a wire of length l , radius of cross-section r and resistivity rho . The rate of heat generation is

A conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b . The resistivity of the material is rho . Find the resistance of the conductc across its ends.

A long cylindrical conductor of cross-sectional area A and radius a is made of material whose resistivity depends only on a distance r from the axis of conductor, given by rho = c/r^(2) , where c is a constant. Find the resistance per unit length of the conductor and the electric field strength due to which a current I flows in it.

Charge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be

The hollow cylinder of length l and inner and outer radius R_1 and R_2 respectively. Find resistance of cylinder if current flows radially outward in the cylinder. Resistivity of material of cylinder id rho .

A thin rod AB of length a has variable mass per unit length rho_(0) (1 + (x)/(a)) where x is the distance measured from A and rho_(0) is a constant. Find the mass M of the rod.