Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
HC VERMA-WORK AND ENERGY-Exercises
- Consider the situation shown in figure. Initially the spring is unstre...
Text Solution
|
- A block of mass m is attached to two unstretched springs of spring con...
Text Solution
|
- A block of mass m sliding n a smooth horizontal surface with velocity...
Text Solution
|
- A small block of mass 100 g is pressed against a horizontal spring fix...
Text Solution
|
- A small hevy block is attached to the lower4 end of a light rod of len...
Text Solution
|
- Figure shows two block A and B, each having a mass of 320 g connected ...
Text Solution
|
- one end of a spring of natural length h and spring constant k is fixed...
Text Solution
|
- Figure shows a light rod of length l rigidly attached to a small heavy...
Text Solution
|
- The bob of a pendulum at rest is given a sharp hit to impart a horizon...
Text Solution
|
- A simple pendulum consists of a 50 cm long string connected to a 100 g...
Text Solution
|
- Figure shows a smooth track, a part of which is a circle of radius R. ...
Text Solution
|
- The bob of a stationary pendulum is given a sharp hit to impart it a h...
Text Solution
|
- A heavy particle is usspended by a 1.5 m long string . It is given a h...
Text Solution
|
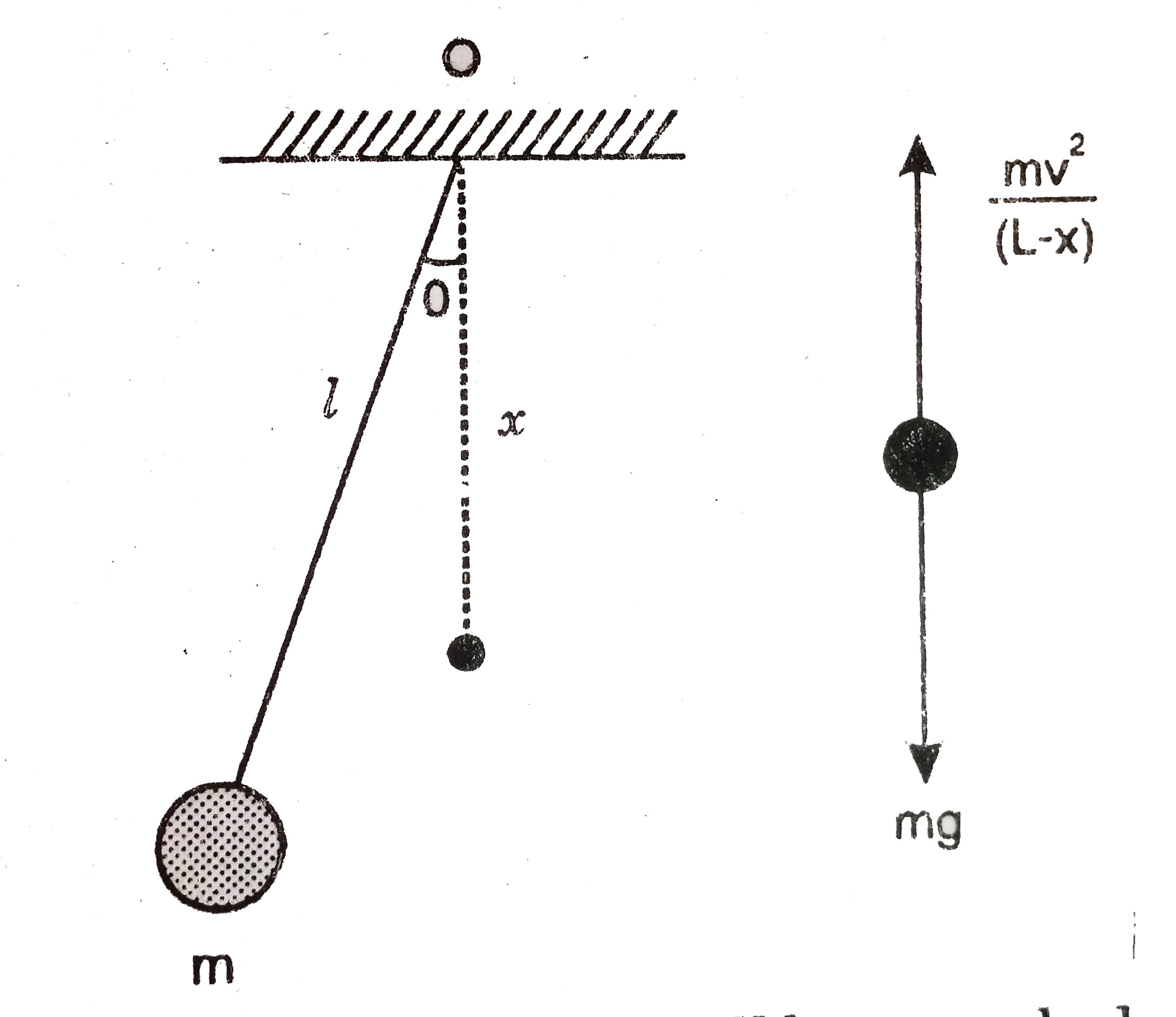
- A simple pendulum of length L having a bob of mass m is deflected from...
Text Solution
|
- A particle slides on the surface of a fixed smooth sphere starting fro...
Text Solution
|
- A particle of mass m is kept on a fixed, smooth sphere of radius R at ...
Text Solution
|
- A particle of mass m is kept on the top of a smooth sphere of radius R...
Text Solution
|
- Figure shows a smooth track which consists of a straight inclined part...
Text Solution
|
- AS chain of length l and mass m lies o the surface of a smooth sphere ...
Text Solution
|
- A smooth sphere of radius R is made to translate line with a constant ...
Text Solution
|