Text Solution
Verified by Experts
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
HC VERMA|Exercise Question for short Answer|17 VideosSIMPLE HARMONIC MOTION
HC VERMA|Exercise Objective -1|21 VideosSIMPLE HARMONIC MOTION
HC VERMA|Exercise Exercises|58 VideosROTATIONAL MECHANICS
HC VERMA|Exercise Exercises|86 VideosSOME MECHANICAL PROPERTIES OF MATTER
HC VERMA|Exercise Exercises|32 Videos
Similar Questions
Explore conceptually related problems
HC VERMA-SIMPLE HARMONIC MOTION-worked out Examples
- A particle executing simple harmonic motion has angular frequency 6.28...
Text Solution
|
- A particle executes a simple harmonic motion of time period T. Find th...
Text Solution
|
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|
- A particle suspended from a vertical spring oscillates 10 times per s...
Text Solution
|
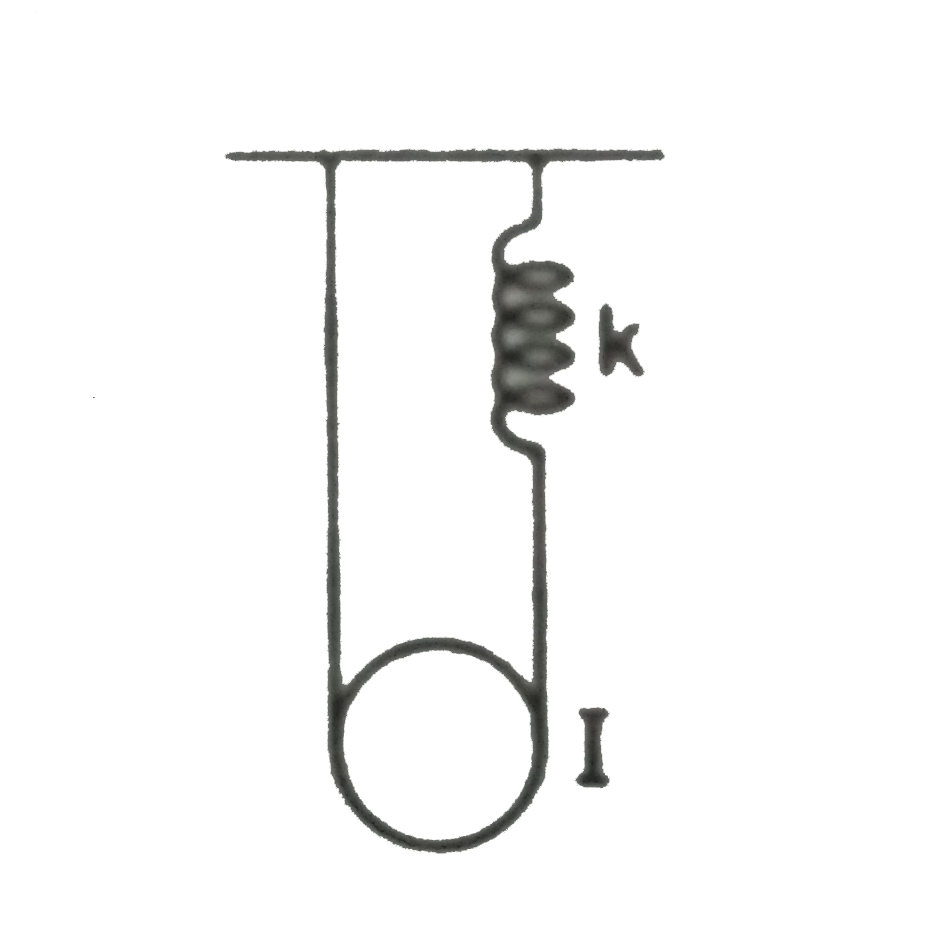
- The pulley shown in figure has a moment of inertias I about its axis a...
Text Solution
|
- Find the blanks:
Text Solution
|
- The left block in filgure collides inelastically with the right block ...
Text Solution
|
- Describe the motion of the mass m shown in figure. The walls and the b...
Text Solution
|
- A block of mass m is suspended from the ceiling of a stationary standi...
Text Solution
|
- The spring as shown in figure is kept in a stretched position with ext...
Text Solution
|
- Assume that as narrow tunnel is dug between two diametrically opposite...
Text Solution
|
- A simple pendulum of length 40 cm oscillates with an angular amplitude...
Text Solution
|
- A simple pendulum having a bob of mass m under goes small oscillations...
Text Solution
|
- A simple pendulum is taken at a place where its separation from the ea...
Text Solution
|
- A simple pendulum is suspended from the ceiling a car accelerating uni...
Text Solution
|
- A uniform meter stick is suspended through a small pin hole at the 10 ...
Text Solution
|
- The moment of inertia of the disc used in a torsional pendulum about t...
Text Solution
|
- A uniform rod of mass m and length l is suspended through a light wire...
Text Solution
|
- A particle is subjected to two simple harmonic motions x1=A1 sinomeg...
Text Solution
|
- A particle is subjected to two simple harmonic motions in the same dir...
Text Solution
|