Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
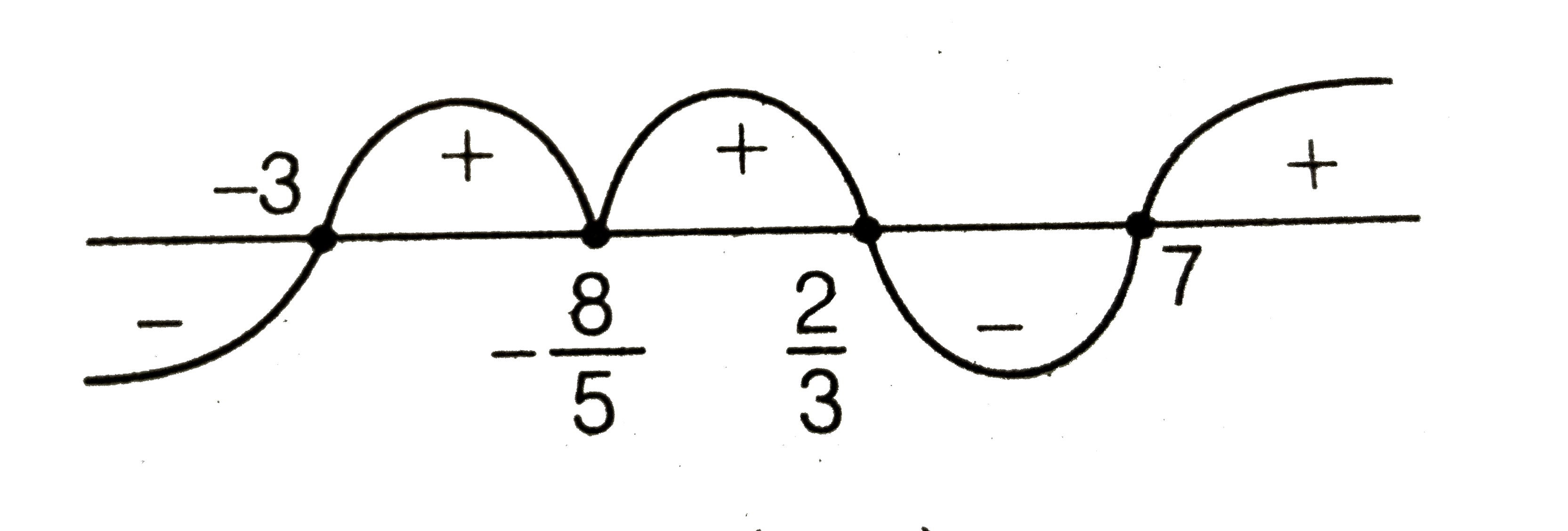
- Solve the inequality (x+3)(3x-2)^5(7-x)^3(5x+8)^2 >= 0.
Text Solution
|
- Solve the inequality if f(x)=((x-2)^(10)(x+1)^(3)(x-((1)/(2)))^(5)(x+8...
Text Solution
|
- Solve the inequality (x^(2)-3x+2)(x^(3)-3x^(2))(4-x^(2))>=0
Text Solution
|
- Solve the following linear inequation in R : x/5<(3x-2)/4-(5x-3)/5
Text Solution
|
- Solve the inequation: 3(x-2)le5x+8
Text Solution
|
- Solve the following systems of linear inequations: 5x -7 lt3(x+3),1-...
Text Solution
|
- निम्नलिखित असमिका निकाय को हल करें । 5x - 7 lt 3 ( x + 3 ) , 1 - (3x...
Text Solution
|
- निम्नलिखित असमिकाओं को हल करें (i) 3x-10 gt 5x+1 (ii) 3(x-2) le 5x...
Text Solution
|
- असमिका को हल कीजिए : (5x+7)/(x-2) lt 3( x ne 2)
Text Solution
|