A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Roots of equation x^(2)-2x+1=0 are:
Text Solution
|
- FInd the roots of the equation 2x^(2)-x+(1)/(8)=0
Text Solution
|
- If alpha,beta are the roots of the equations ax^(2)+bx+c=0 then the ro...
Text Solution
|
- The equations x^(2)-2x+1=0,x^(2)-3x+2=0 have a common root then that c...
Text Solution
|
- If alpha, beta are the roots of the equation 2x^(2)-x-1=0 then form th...
Text Solution
|
- One root of the equdratic equation x^(2)+2x+1=0 is
Text Solution
|
- The quadratic equation x^(2)-2x+1=0 have no real root.
Text Solution
|
- The roots of the quadratic equation x^(2)-2x+1=0 are and .
Text Solution
|
- Determine the nature of the roots of the equation 2x^(2) + x - 1 = 0
Text Solution
|
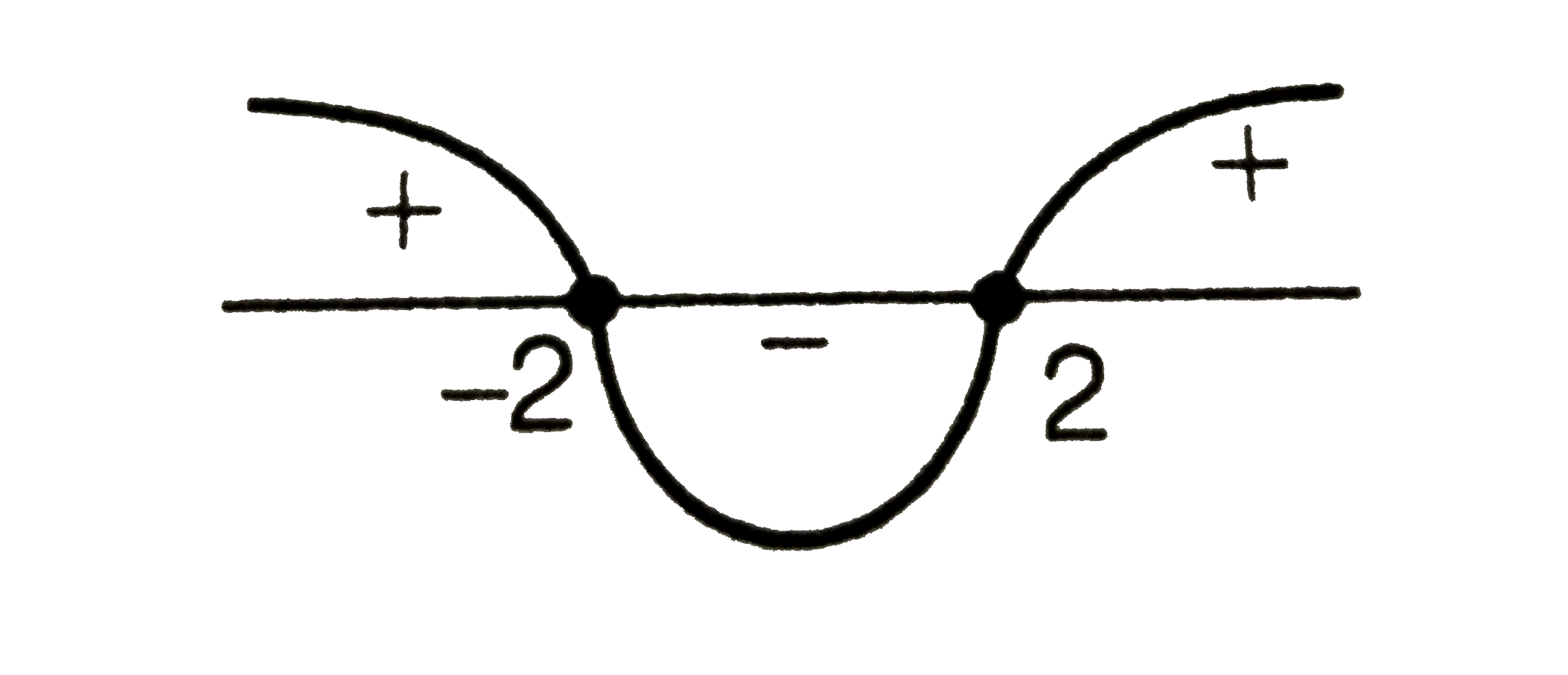 ltBrgt (i) Consider `Dge0(-m)^(2)-4.1.4ge0`
ltBrgt (i) Consider `Dge0(-m)^(2)-4.1.4ge0`