Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
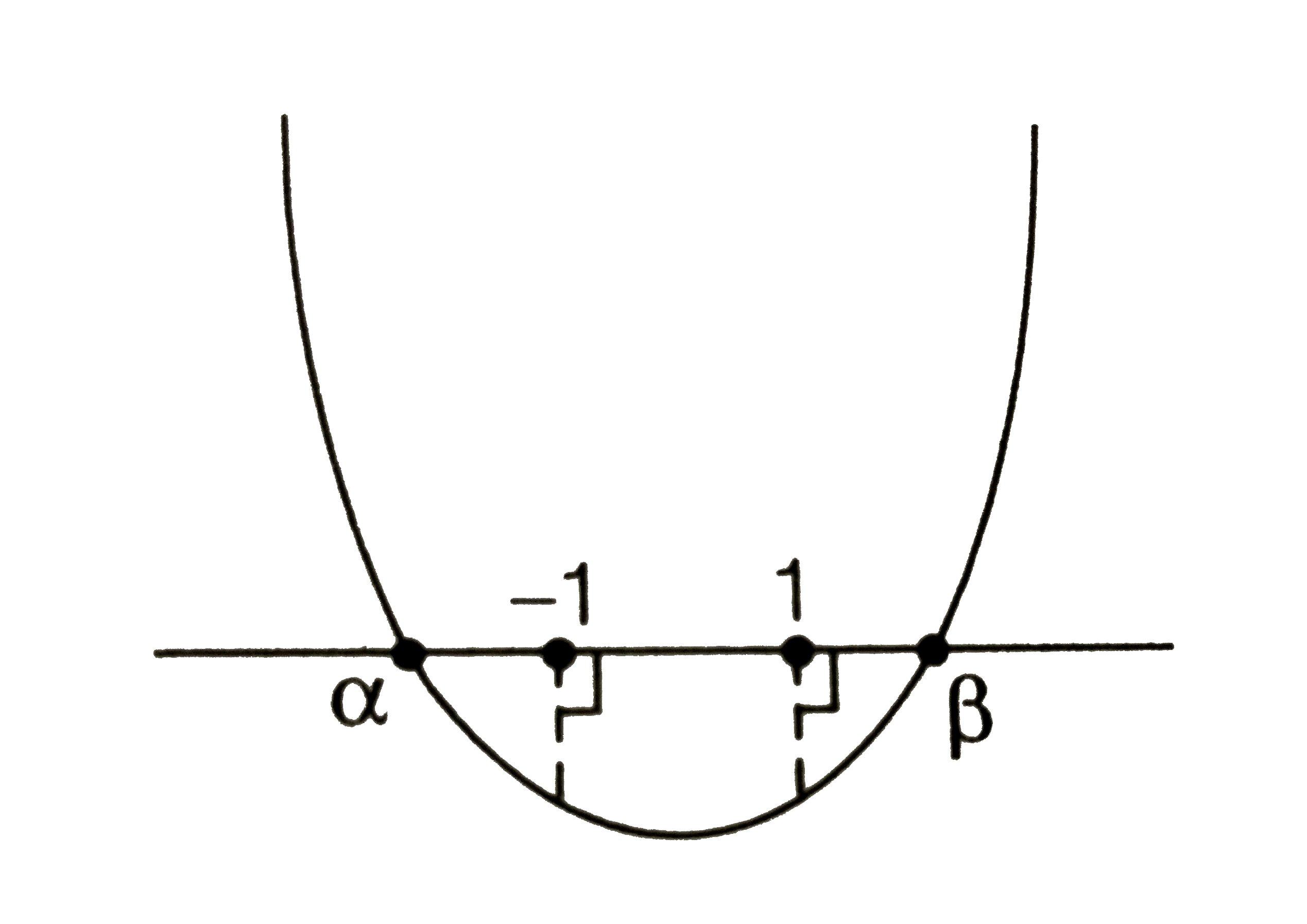
- Let a, b, c be real. If a x^(2)+b x+c=0 has two real roots alpha and...
Text Solution
|
- Let a, b, c be real. If a x^2+b x+c=0 has two real roots alpha and bet...
Text Solution
|
- If alpha,beta are non-real roots of ax^(2)+bx+c=0,(a,b,c in R), then (...
Text Solution
|
- Let alpha and beta (a lt beta) " be the roots of the equation " x^(2...
Text Solution
|
- Let alpha and beta (a lt beta) " be the roots of the equation " x^(2...
Text Solution
|
- Let a,b,c in R and a gt 0. If the quadratic equation ax^(2) +bx +c=...
Text Solution
|
- Let a,b,c be real if ax^(2)+bx+c=0 has two real roots alpha and beta w...
Text Solution
|
- IF alpha , beta are the roots of the equation ax^2 + bx +c=0 ...
Text Solution
|
- माना a,b,c वास्तविक है| यदि ax^(2) + bx +c=0 के दो वास्तविक मूल alpha ...
Text Solution
|