Find the cube of `(2a-3b)`
Find the cube of `(2a-3b)`
Text Solution
Verified by Experts
The correct Answer is:
(i) `m epsilong (-oo,(7-sqrt(3))/2)` (ii) `m epsilon ((7+sqrt(33))/2,oo)` (iii) `m epsilon phi`
(iv) `m epsilon ((7-sqrt(3))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) `m epsilon (0,3)` (vi) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)`
(vii) `m epsilon ((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)uu((7+sqrt(3))/2,oo)`
(ix) `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33)/2,(7+sqrt(33))/2)`
(x) `m epsilon `((11-sqrt(73))/2,(7+sqrt(3))/2)`
(iv) `m epsilon ((7-sqrt(3))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) `m epsilon (0,3)` (vi) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)`
(vii) `m epsilon ((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)uu((7+sqrt(3))/2,oo)`
(ix) `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33)/2,(7+sqrt(33))/2)`
(x) `m epsilon `((11-sqrt(73))/2,(7+sqrt(3))/2)`
`:'2x^(2)-2(2m+1)x+m(m+1)=0 [:'m epsilonR]`
`:.D=[-2(2m+1)]^(2)-8m(m+1)[D=b^(2)-4ac]`
`=4{(2m+1)^(2)-2m(m+1)}`
`=4(2m^(2)+2m+1)`
`=8(m^(2)+m+1/2)=8{(m+1/2)^(2)+1/4}gt0`
or `D gt0, AA m epsiolonR`……i
x coordinate of vertex `=-b/(2a)=(2(m+1))/4=(m+1/2)`.....ii
and let
`f(x)=x^(2)-(2m+1)x+1/2m(m+1)` ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I `Dge0`
`:. m epsilonR` [from Eq. (i) ]
CaseII x-coordinate of vertex `lt2`.
`impliesm+1/2lt0` [from Eq. (ii) ]
or `mlt3/2`
Case III `f(2)gt0`
`implies4-(2m+1)2+1/2m(m+1)gt0`
`impliesm^(2)-7m+4gt0`
`:.m epsilon(-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)`
Combining all cases we get
`m epsilon (-oo,(7-sqrt(3))/2)`
(ii) Both roots are greater than 2.
Consider the following cases.
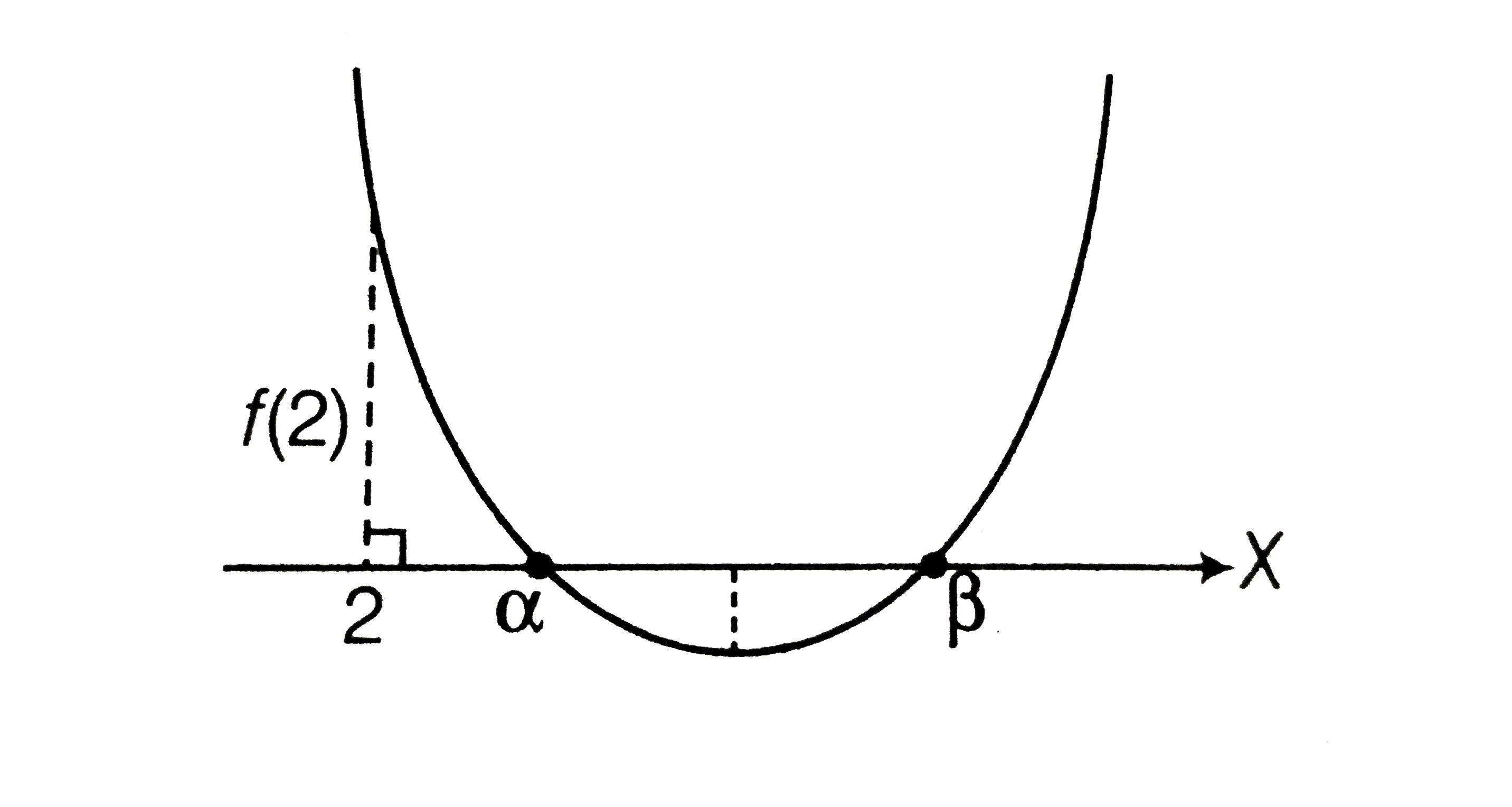
Case I `Dge0`
`:. m epsilon R`[from Eq. (i)]
Case II x- coordinate of vertex `gt2`
`impliesm+1/2gt2`[ from Eq. (ii)]
`:.m gt3/2`
Case III `f(2)gt0`
`m epsilon (-oo,(7-sqrt(33))/2)uu(7+(sqrt(33))/2,oo)` [from part (a) ]
Combining all cases, we get
`m epsilon ((7+sqrt(33))/2,oo)`
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I `Dge0`
`:. m epsilonR` [from Eq. (i)]
Case II `f(2)gt0`
`:. m epsilon (-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)` [from part (a)]
Case Case III `f(3)gt0`
`implies9-3(2m+1)+1/2m(m+1)gt0`
or `m^(2)-11m+12gt0`
`:m epsilon (-oo,(11-sqrt(73))/2)uu((11+sqrt(73))/2,oo)`
Case IV `2ltx` -coordinate of vertex `lt3`
`implies2ltm+1/2lt3`
or `3/2ltmlt5/2` or `m epsilon (3/2,5/2)`
Combining allcases we get
`m epsilon phi`
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I `Dgt0`
`:.m epsilon R` [from Eq (i) ]
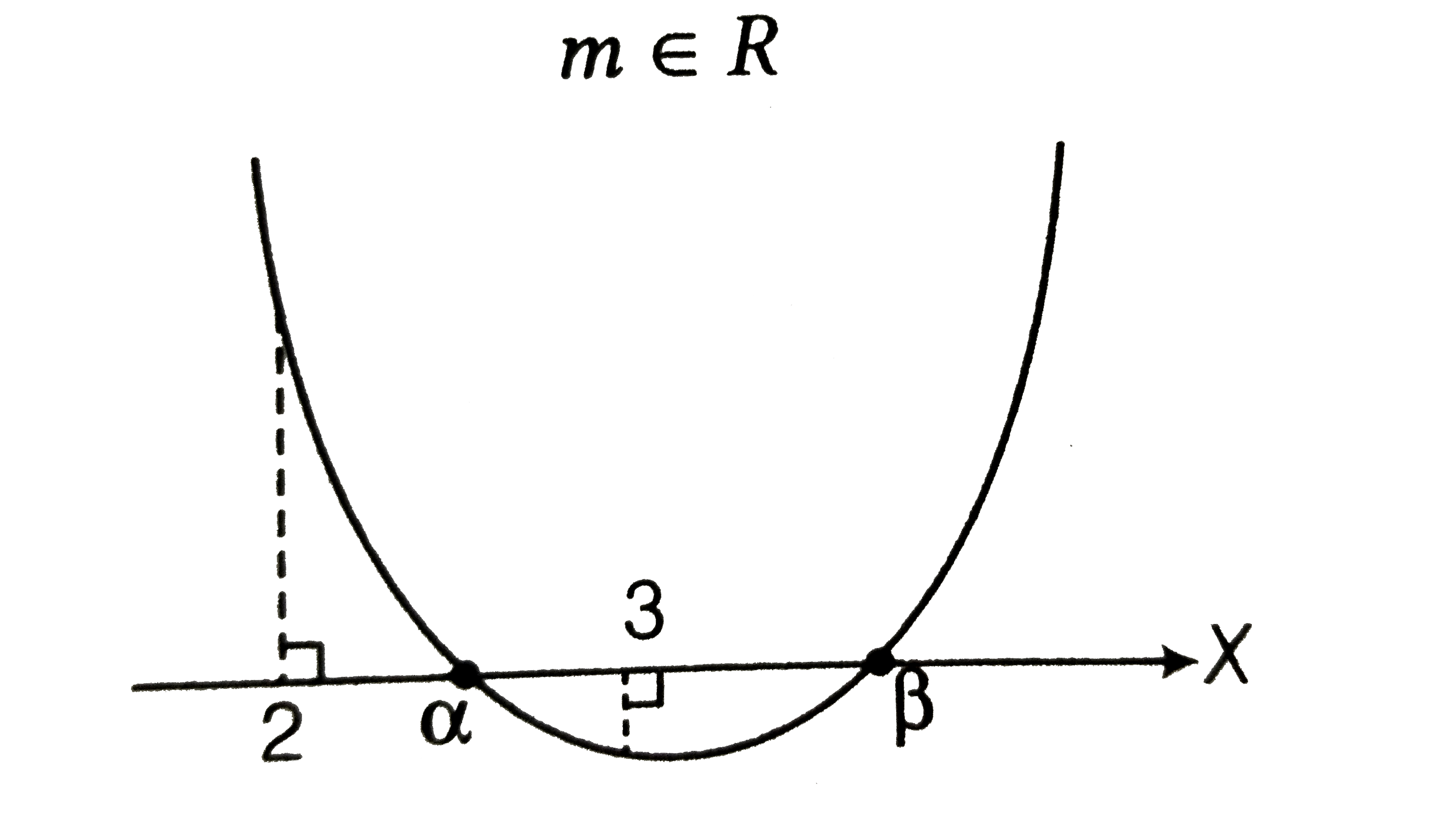
Case II `f(2)f(3)lt0`
`(4-2(2m+1)+1/2m(m+1))`
`(9-3(2m+1)+1/2m(m+1))lt0`
`implies(m^(2)-7m+4)(m^(2)-11m+12)lt0`
`implies(m-(7-sqrt(33))/2)(m-(7+sqrt(33))/2)`
`(m-(11-sqrt(73))/2)(m-(11+sqrt(73))/2)lt0`
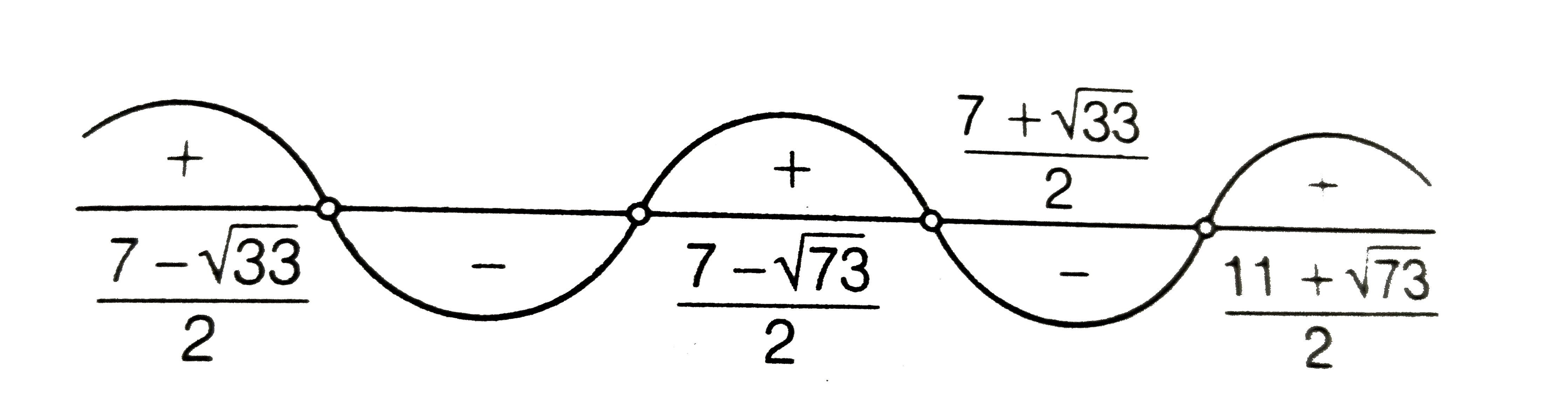
`:. m epsilon ((7-sqrt(33))/2,(11-sqrt(33))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon `((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) One root is smaller than 1 and the other root is greater than 1.
Consiser the following cases.
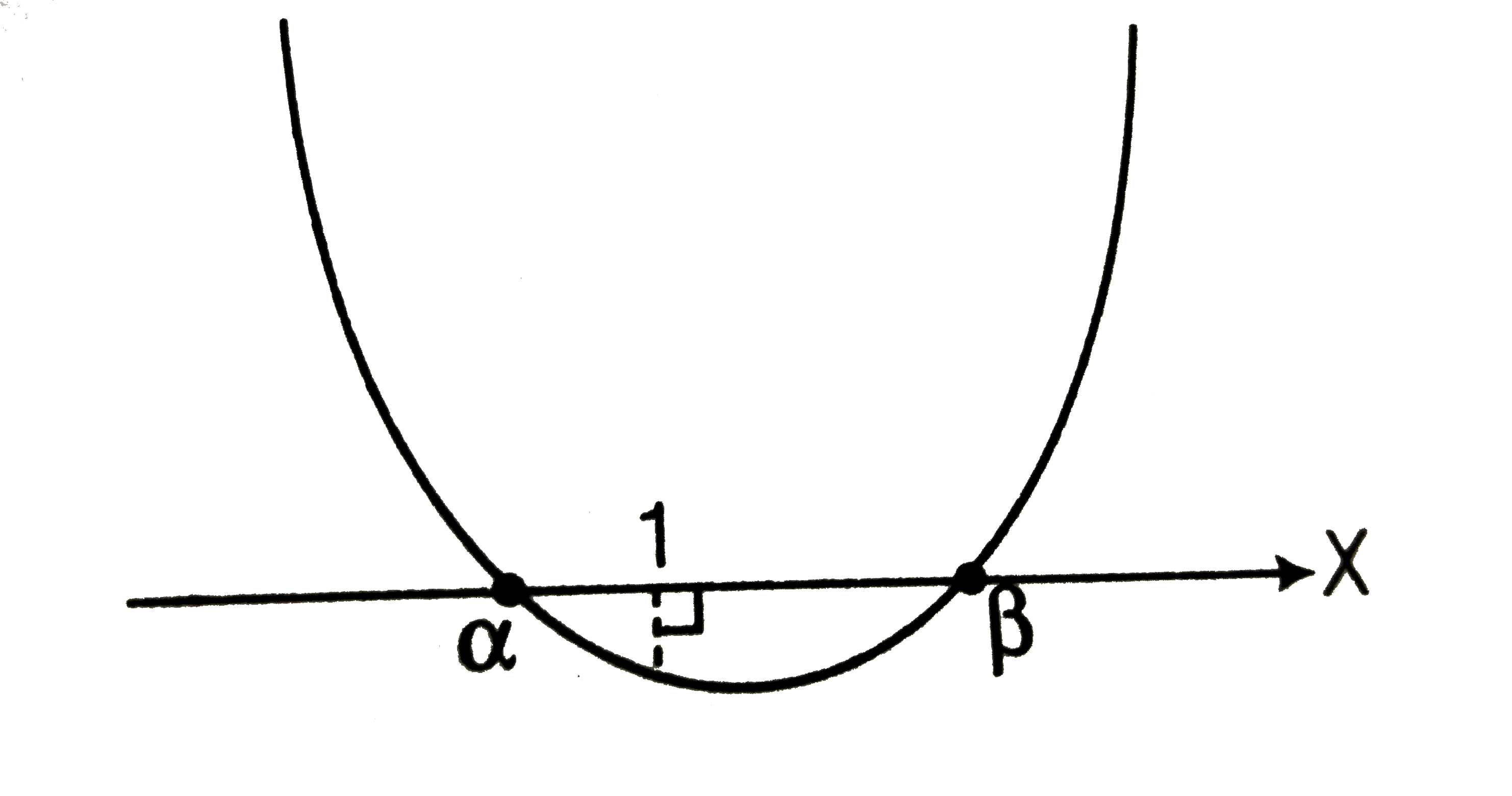
Case I `Dgt0`
`:.m epsilonR` [from Eq. (i)]
Case II `f(1)lt0`
`implies1-(2+1)+1/2m(m+1)lt0` [from Eq. (iii) ]
`impliesm^(2)-3mlt0`
`impliesm(m-3)lt0`
`:.m epsilon (0,3)`
Combining both cases we get
` m epsilon(0,3)`
(vi) One root is greater than 3 and the other root is smaller than 2. ltbRgt Consiser the following cases
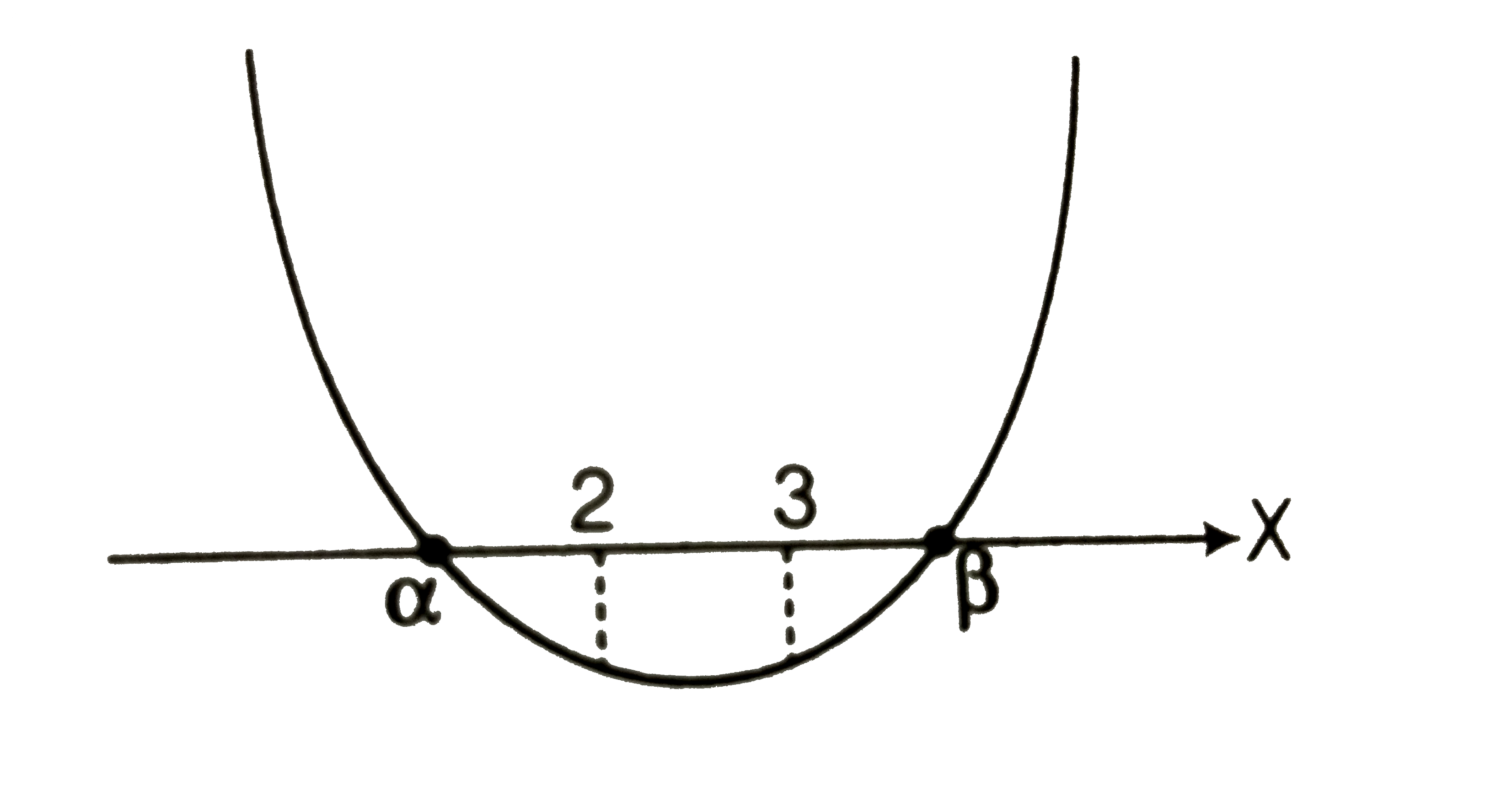
Case I `Dgt0`
`:. m epsion R` [from Eq. (i) ]
Case II `f(2)lt0`
`impliesm^(2)-8m+4lt0`
`:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2`
`:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2`
`:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2`
`:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)`
(vii) Atleast one root lies in the interval (2,3).
i.e. (d) `uu` (c)
`:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) At least one root is greater than 2.
i.e (Exactly one root is greater than 2) `uu` (Both roots are greater 2).
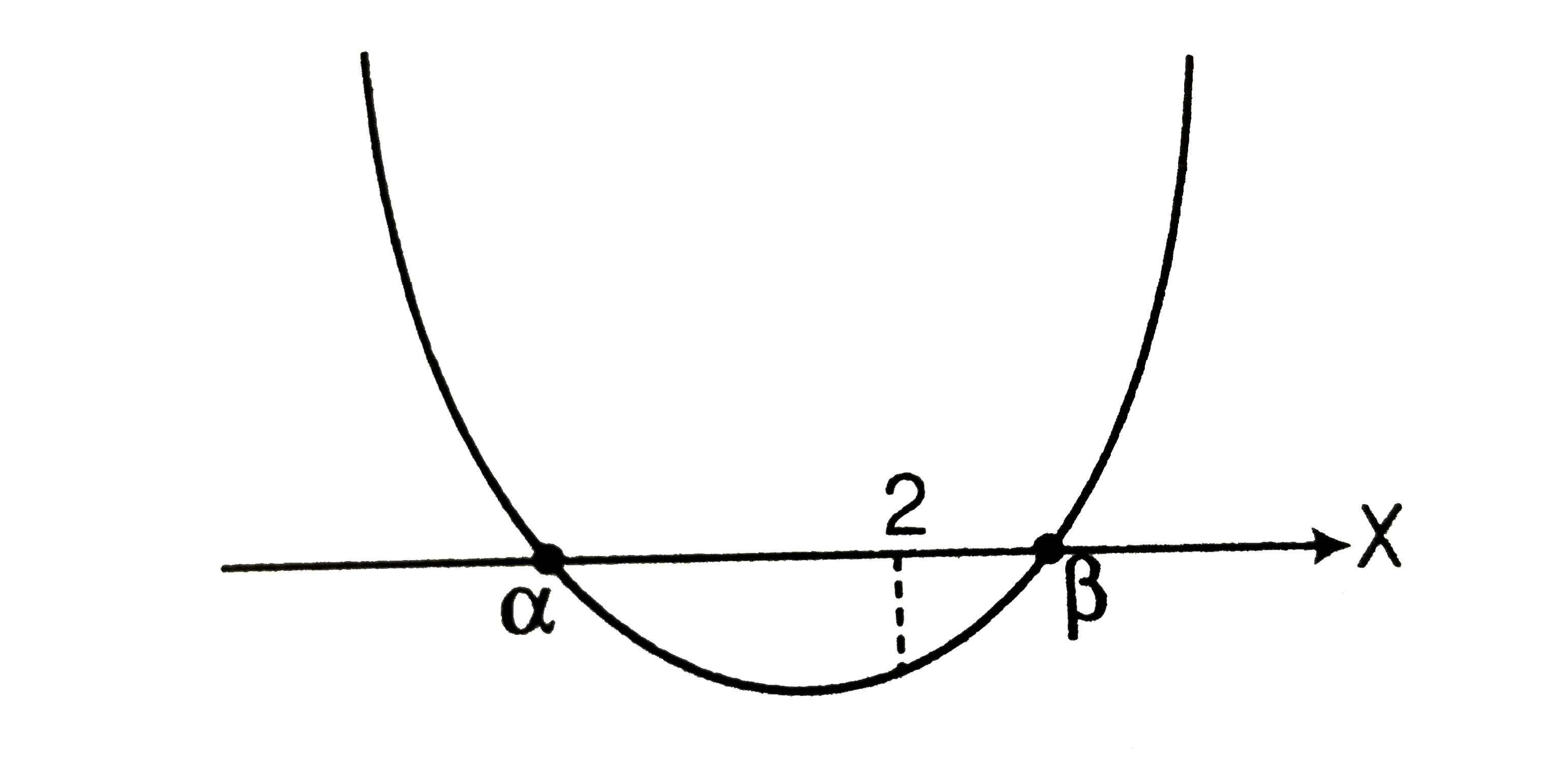
of (Exactly one root is greater than 2) `uu` (b)…..i
Consider the following cases:
Case I `Dgt0`
`:. m epsilon`[from Eq. (i)]
Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Combining both cases we get
`m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`………ii
Finally from Eqs i and ii we get
` m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)`
(ix) Atleast one root is smaller than 2.
i.e (Exactly one root is smaller then 2) `uu` (Both roots are smaller than2)
or (h) II `uu`(a)
We get `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)`
(x) Both 2 and 3 lie between `alpha` and `beta`
Consider the following cases:
Case `Dgt0`
`:. mepsilonR` [from Eq (i)]
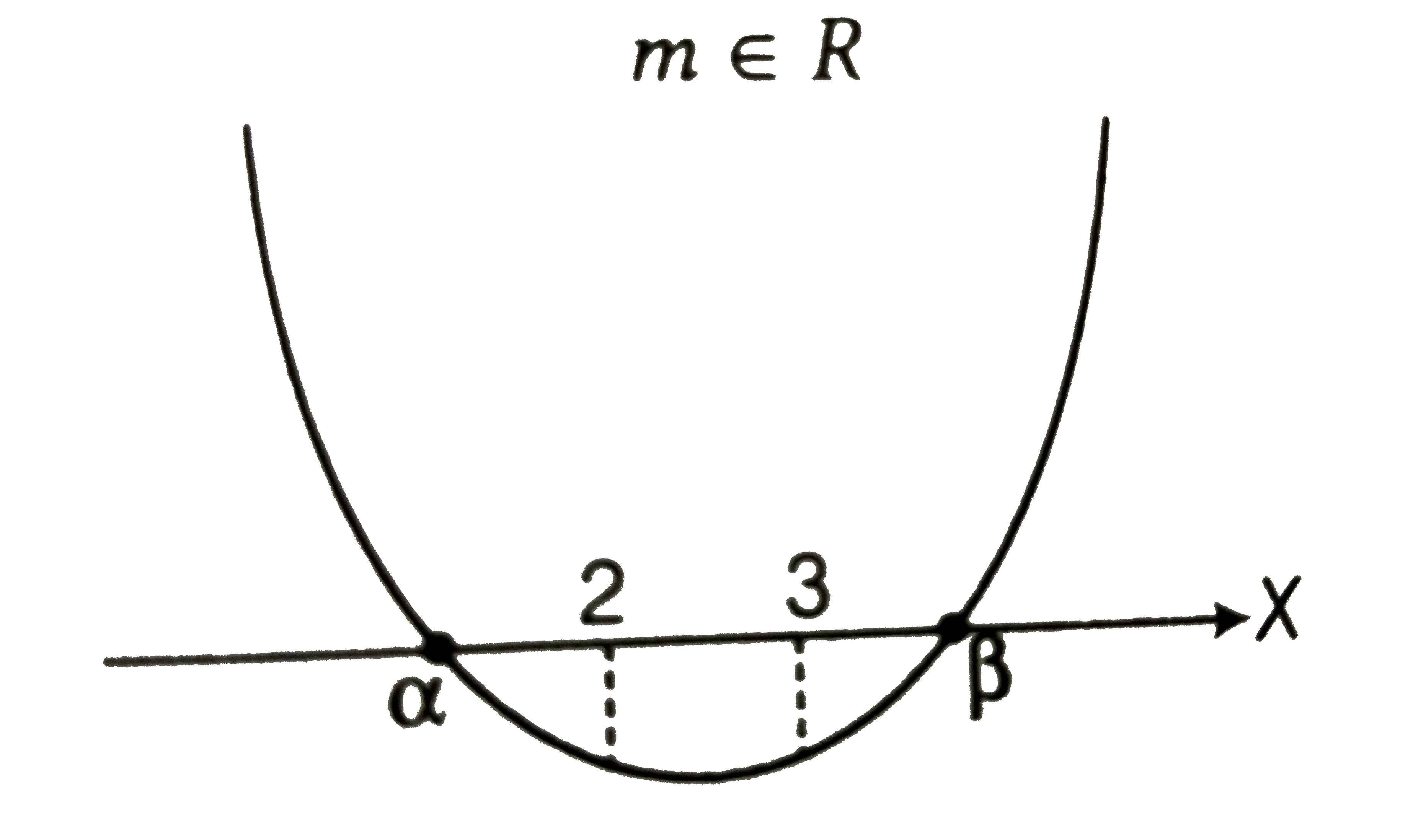
Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)`
`:.D=[-2(2m+1)]^(2)-8m(m+1)[D=b^(2)-4ac]`
`=4{(2m+1)^(2)-2m(m+1)}`
`=4(2m^(2)+2m+1)`
`=8(m^(2)+m+1/2)=8{(m+1/2)^(2)+1/4}gt0`
or `D gt0, AA m epsiolonR`……i
x coordinate of vertex `=-b/(2a)=(2(m+1))/4=(m+1/2)`.....ii
and let
`f(x)=x^(2)-(2m+1)x+1/2m(m+1)` ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I `Dge0`
`:. m epsilonR` [from Eq. (i) ]
CaseII x-coordinate of vertex `lt2`.
`impliesm+1/2lt0` [from Eq. (ii) ]
or `mlt3/2`
Case III `f(2)gt0`
`implies4-(2m+1)2+1/2m(m+1)gt0`
`impliesm^(2)-7m+4gt0`
`:.m epsilon(-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)`
Combining all cases we get
`m epsilon (-oo,(7-sqrt(3))/2)`
(ii) Both roots are greater than 2.
Consider the following cases.

Case I `Dge0`
`:. m epsilon R`[from Eq. (i)]
Case II x- coordinate of vertex `gt2`
`impliesm+1/2gt2`[ from Eq. (ii)]
`:.m gt3/2`
Case III `f(2)gt0`
`m epsilon (-oo,(7-sqrt(33))/2)uu(7+(sqrt(33))/2,oo)` [from part (a) ]
Combining all cases, we get
`m epsilon ((7+sqrt(33))/2,oo)`
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I `Dge0`
`:. m epsilonR` [from Eq. (i)]
Case II `f(2)gt0`
`:. m epsilon (-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)` [from part (a)]
Case Case III `f(3)gt0`
`implies9-3(2m+1)+1/2m(m+1)gt0`
or `m^(2)-11m+12gt0`
`:m epsilon (-oo,(11-sqrt(73))/2)uu((11+sqrt(73))/2,oo)`
Case IV `2ltx` -coordinate of vertex `lt3`
`implies2ltm+1/2lt3`
or `3/2ltmlt5/2` or `m epsilon (3/2,5/2)`
Combining allcases we get
`m epsilon phi`
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I `Dgt0`
`:.m epsilon R` [from Eq (i) ]

Case II `f(2)f(3)lt0`
`(4-2(2m+1)+1/2m(m+1))`
`(9-3(2m+1)+1/2m(m+1))lt0`
`implies(m^(2)-7m+4)(m^(2)-11m+12)lt0`
`implies(m-(7-sqrt(33))/2)(m-(7+sqrt(33))/2)`
`(m-(11-sqrt(73))/2)(m-(11+sqrt(73))/2)lt0`
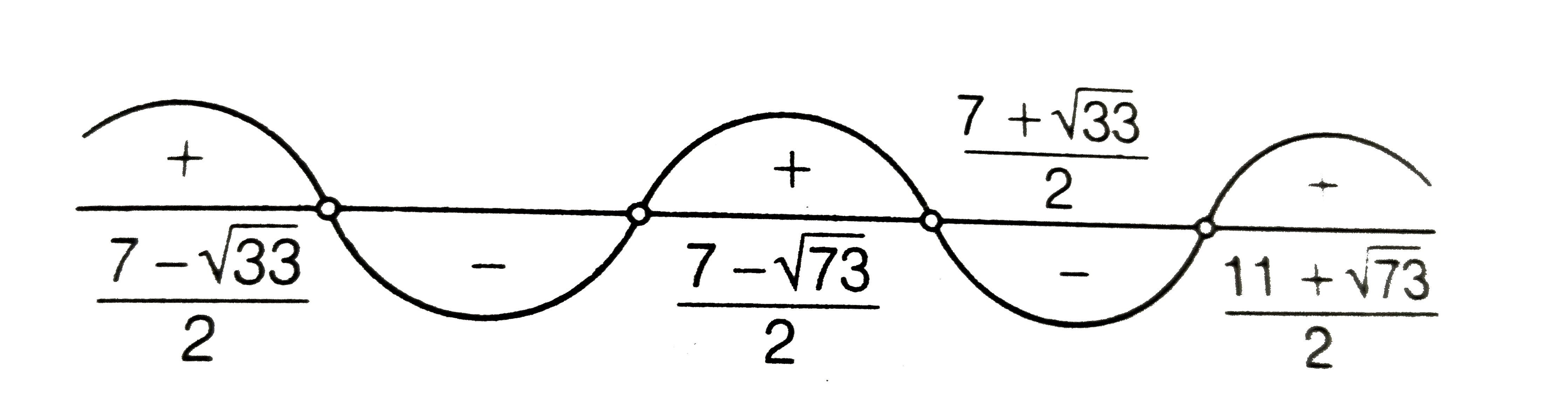
`:. m epsilon ((7-sqrt(33))/2,(11-sqrt(33))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon `((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) One root is smaller than 1 and the other root is greater than 1.
Consiser the following cases.

Case I `Dgt0`
`:.m epsilonR` [from Eq. (i)]
Case II `f(1)lt0`
`implies1-(2+1)+1/2m(m+1)lt0` [from Eq. (iii) ]
`impliesm^(2)-3mlt0`
`impliesm(m-3)lt0`
`:.m epsilon (0,3)`
Combining both cases we get
` m epsilon(0,3)`
(vi) One root is greater than 3 and the other root is smaller than 2. ltbRgt Consiser the following cases

Case I `Dgt0`
`:. m epsion R` [from Eq. (i) ]
Case II `f(2)lt0`
`impliesm^(2)-8m+4lt0`
`:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2`
`:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2`
`:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2`
`:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)`
(vii) Atleast one root lies in the interval (2,3).
i.e. (d) `uu` (c)
`:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) At least one root is greater than 2.
i.e (Exactly one root is greater than 2) `uu` (Both roots are greater 2).

of (Exactly one root is greater than 2) `uu` (b)…..i
Consider the following cases:
Case I `Dgt0`
`:. m epsilon`[from Eq. (i)]
Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Combining both cases we get
`m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`………ii
Finally from Eqs i and ii we get
` m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)`
(ix) Atleast one root is smaller than 2.
i.e (Exactly one root is smaller then 2) `uu` (Both roots are smaller than2)
or (h) II `uu`(a)
We get `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)`
(x) Both 2 and 3 lie between `alpha` and `beta`
Consider the following cases:
Case `Dgt0`
`:. mepsilonR` [from Eq (i)]

Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)`
Similar Questions
Explore conceptually related problems
If the polynomial 7x^(3)+ax+b is divisible by x^(2)-x+1 , find the value of 2a+b.
Find the cube root of 15625 by the prime factorization method.
Find the cube root of each of the following numbers by prime factorization method: 10648
Find the cube root of each of the following numbers by prime factorization method: 13824
Find the cube root of each of the following numbers by prime factorization method: 110592
Find the cube root of each of the following numbers by prime factorization method: 175616
Find the cube root of each of the following numbers by prime factorization method: 64
Find the cube root of each of the following numbers by prime factorization method: 512
Find the cube root of each of the following numbers by prime factorization method: 27000
Find the cube root of each of the following numbers by prime factorization method: 15625
Recommended Questions
- Find the cube of (2a-3b)
Text Solution
|
- निम्नलिखित प्रत्येक व्यंजक के गुणनखण्ड़ कीजिए: (2a+3b)^(2)+2(2a+3b)(2...
Text Solution
|
- If (2a - 3b)/(2a+3b) = 1/3, then find the value of (2a^(3) - 3b^(3))/(...
Text Solution
|
- ಕೆಳಗಿನ ಘನಗಳನ್ನು ವಿಸ್ತ್ರತ ರೂಪದಲ್ಲಿ ಬರೆಯಿರಿ : (2a - 3b)^3
Text Solution
|
- కింది ఘనలను విస్తరించండి. (2a+3b)^(3)
Text Solution
|
- Write the following cube in expanded : (2a-3b)^3.
Text Solution
|
- 2a-3b,2a+3b का माध्य ज्ञात करें।
Text Solution
|
- If A=[[0,2,3],[2,1,4]] "and" B=[[7,6,3],[1,4,5]] "find " 2A+3B,2A-3B.
Text Solution
|
- सरल कीजिए - (2 a - 3b) (2a + 3b)
Text Solution
|