A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
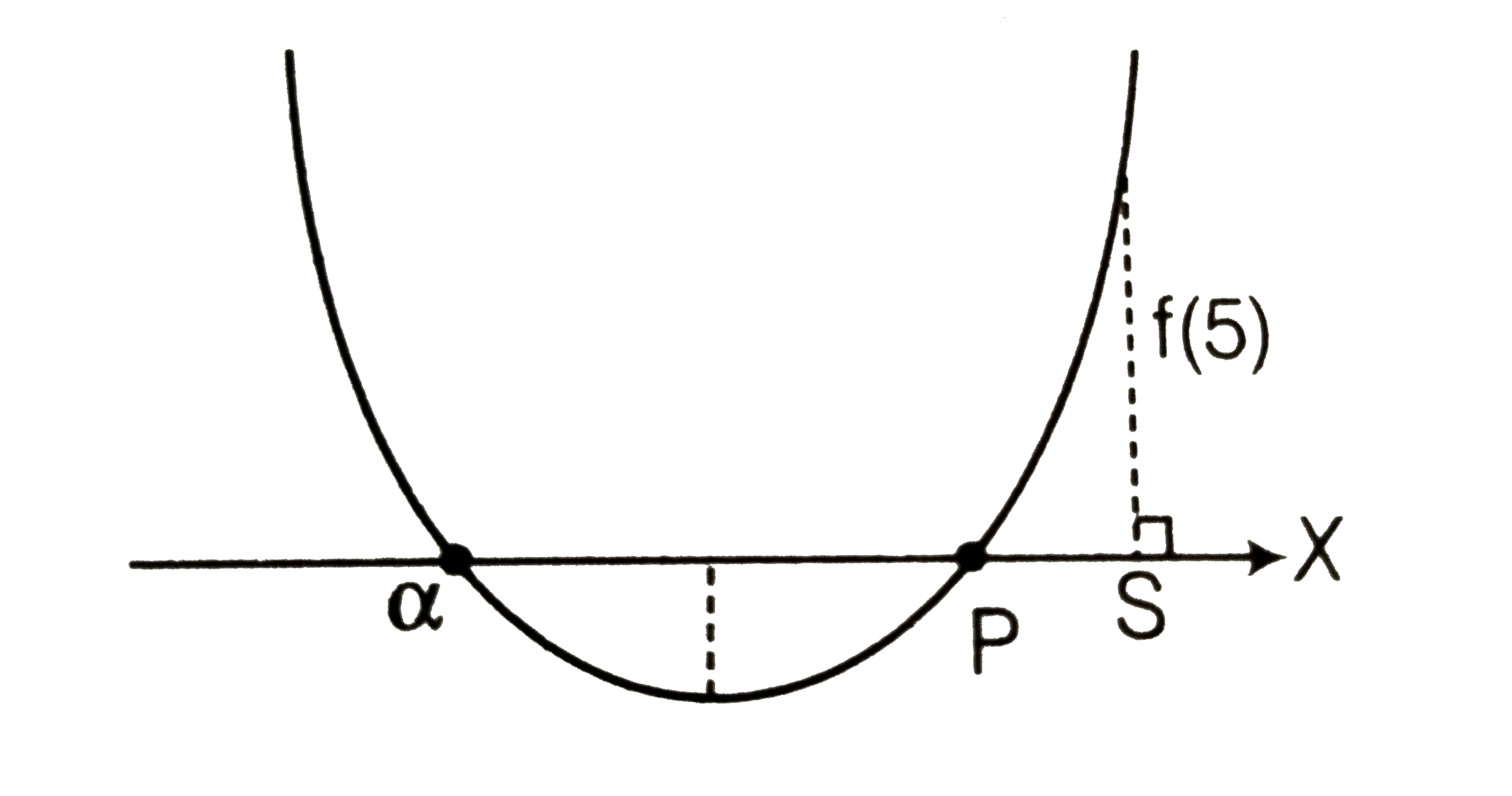
- If both the roots of the quadratic equation x^(2)-2 k x+(k^(2)+k-5)=0 ...
Text Solution
|
- If both the roots of the quadratic equation x^2-2kx+k^2+k-5=0 are less...
Text Solution
|
- If both roots of the quadratic equation x^(2)+x(4-2k)+k^(2)-3k-1=0 are...
Text Solution
|
- यदि द्विघातीय समीकरण x^(2)-2kx+k^(2)+k-5=0 के दोनों मूल 5 से कम है तो ...
Text Solution
|
- यदि द्विघात समीकरण x^(2)-2kx+k^(2)+k-5=0 के दोनों मूल 5 से छोटे...
Text Solution
|
- IF both the roots of the quadratic equation x^2-2kx+k^2 +k -5=0 a...
Text Solution
|
- Let A be the set of values of k for which 2 lies between the roots of ...
Text Solution
|
- If one root is greater than 2 and the other root is less than 2 for th...
Text Solution
|
- If the both the roots of the quadratic equation x^(2)-2kx+k^(2)+k-5=0 ...
Text Solution
|