A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
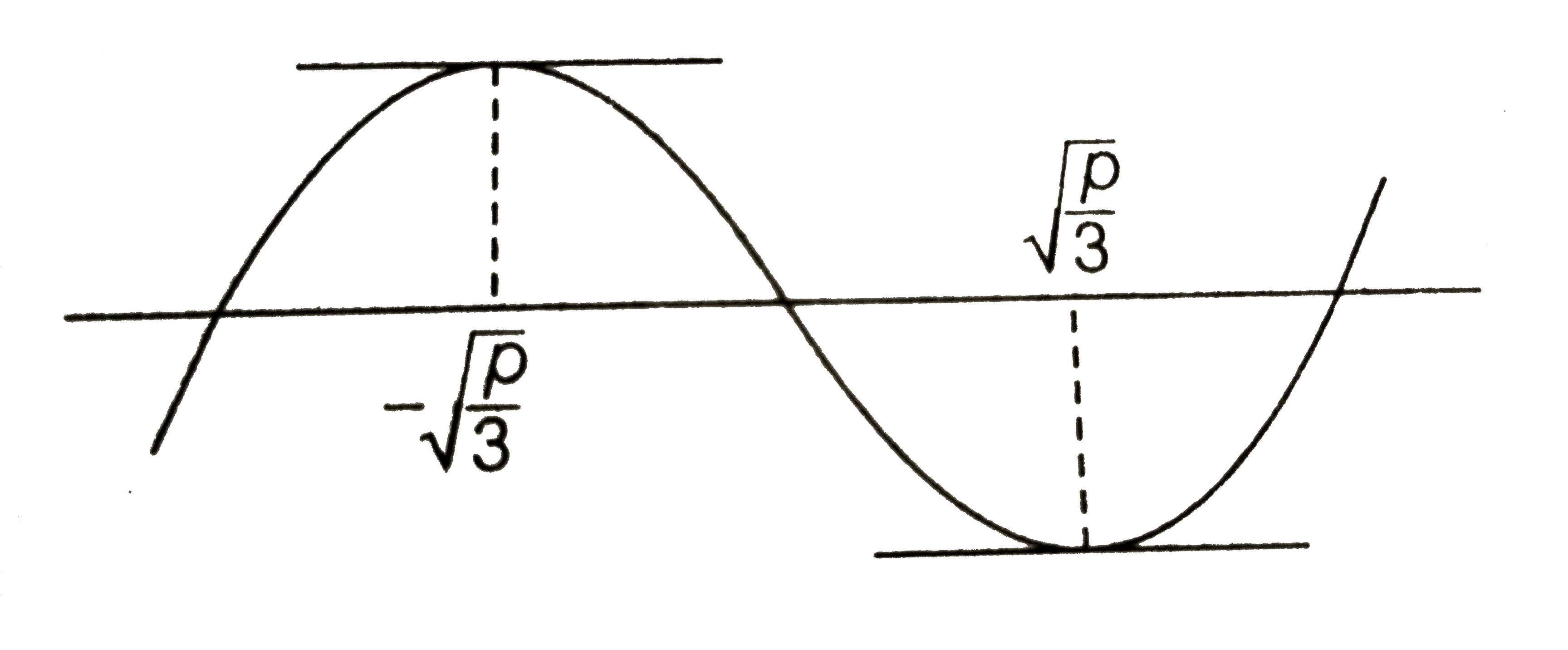
- Suppose the cubic x^(3)-px+q has three distinct real roots, where p gt...
Text Solution
|
- If p and q are distinct primes and x^(2)-px+q=0 has distinct positive ...
Text Solution
|
- If 2 + isqrt3 is a root of x^(3) - 6x^(2) + px + q = 0 (where p and q ...
Text Solution
|
- मान लीजिए घन x^(3) - px + qके तीन विभिन्न मूल है जहाँ p, q gt 0,तब निम...
Text Solution
|
- Suppose the cubic x^(3)-px+q has three distinct real roots, where pgt0...
Text Solution
|
- Suppose the cubic x^3-px+q has three real roots where pgt0 and qgt0 . ...
Text Solution
|
- p and q are distinct prime numbers and if the equation x^2 -px ...
Text Solution
|
- Let 'p' & 'q' be real numbers . Prove that the cubic y = x^(3) + p x +...
Text Solution
|
- If x^(2) - px + q = 0 (p,q in R and p ne 0, q ne 0) has distinct real ...
Text Solution
|