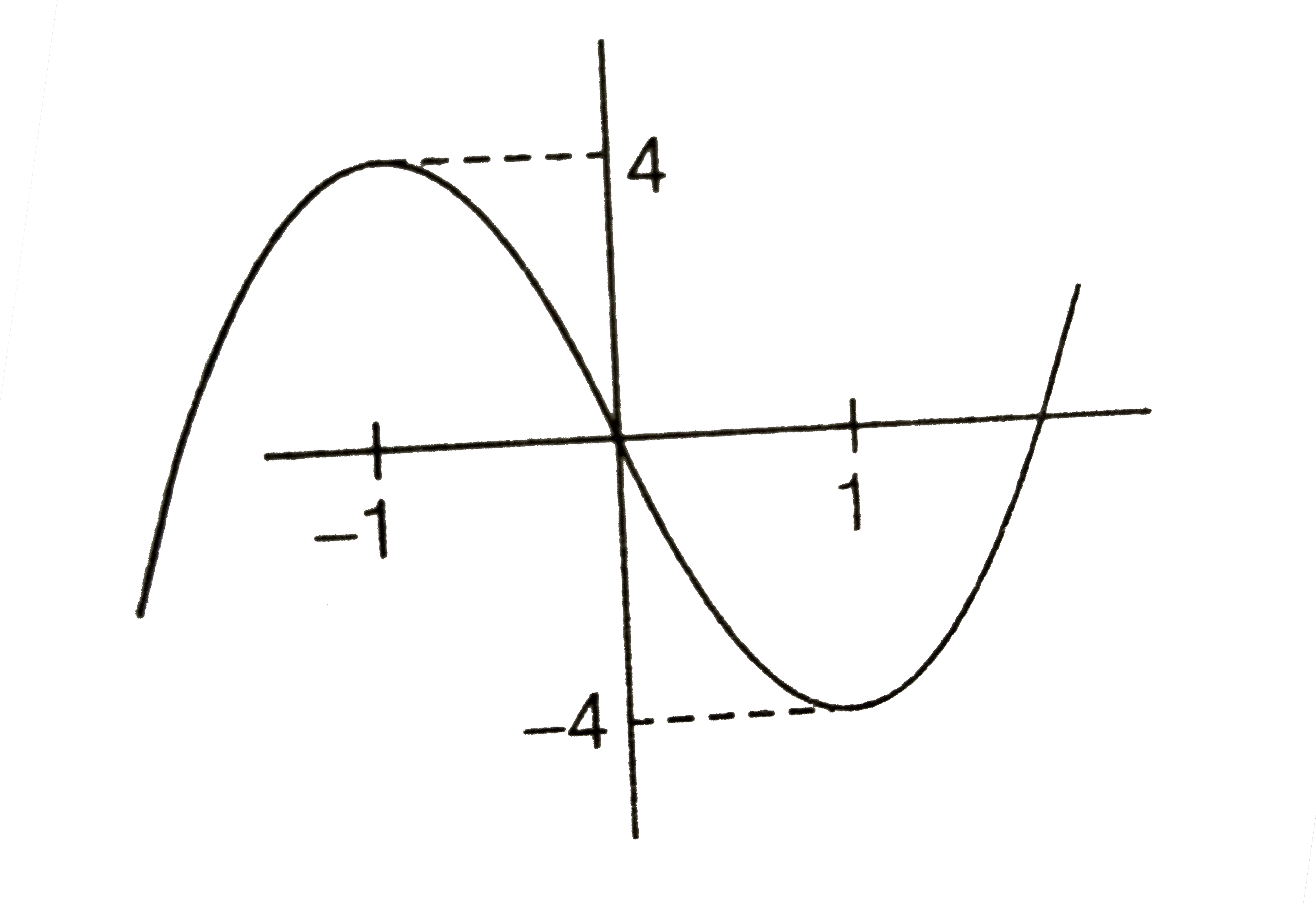
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let a in R and f : R rarr R be given by f(x)=x^(5)-5x+a, then (a) f...
Text Solution
|
- If f(x)=int(x^8+4)/(x^4-2x^2+2)dx and f(0)=0,t h e n (a)f(x) is an...
Text Solution
|
- Late a in R and let f: Rvec be given by f(x)=x^5-5x+a , then f(x) has...
Text Solution
|
- If f(x) is a polynomial of degree 5 with real coefficientssuch that f(...
Text Solution
|
- f(x) is a polynomial function, f: R rarr R, such that f(2x)=f'(x)f''(x...
Text Solution
|
- bb"Statement I" The equation f(x)=4x^(5)+20x-9=0 has only one real roo...
Text Solution
|
- If f(x) is a polynomial of degree 5 with real coefficients such that f...
Text Solution
|
- If f(x) is a real valued polynomial and f (x) = 0 has real and distinc...
Text Solution
|
- Let a in R and let f: Rvec be given by f(x)=x^5-5x+a , then (a) f(x...
Text Solution
|