Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Prove that (n !) is divisible by (n !)^(n-1)!
Text Solution
|
- Prove that (n !+1) is not divisible by any natural number between 2 a...
Text Solution
|
- Prove by the principle of mathematical induction that n(n+1)(2n+1) is ...
Text Solution
|
- Using mathematical induction,prove the following n(n+1)(2n+1),n in N i...
Text Solution
|
- prove that 4^(n)-1 is divisible by 3, for each natural number n.
Text Solution
|
- Prove that (mn)! Is divisible by (n!)^(m) " and" (m!)^(n).
Text Solution
|
- Prove by induction that n(n+1) (2n+1) is divisible by 6.
Text Solution
|
- Prove that for every positive integer n, 1^(n) + 8^(n) - 3^(n) - 6^(n)...
Text Solution
|
- মনে করো, f(n) = n(n + 1)(2n + 1), যদি f(n) সর্বদা 6 দ্বারা বিভাজ্য হয...
Text Solution
|
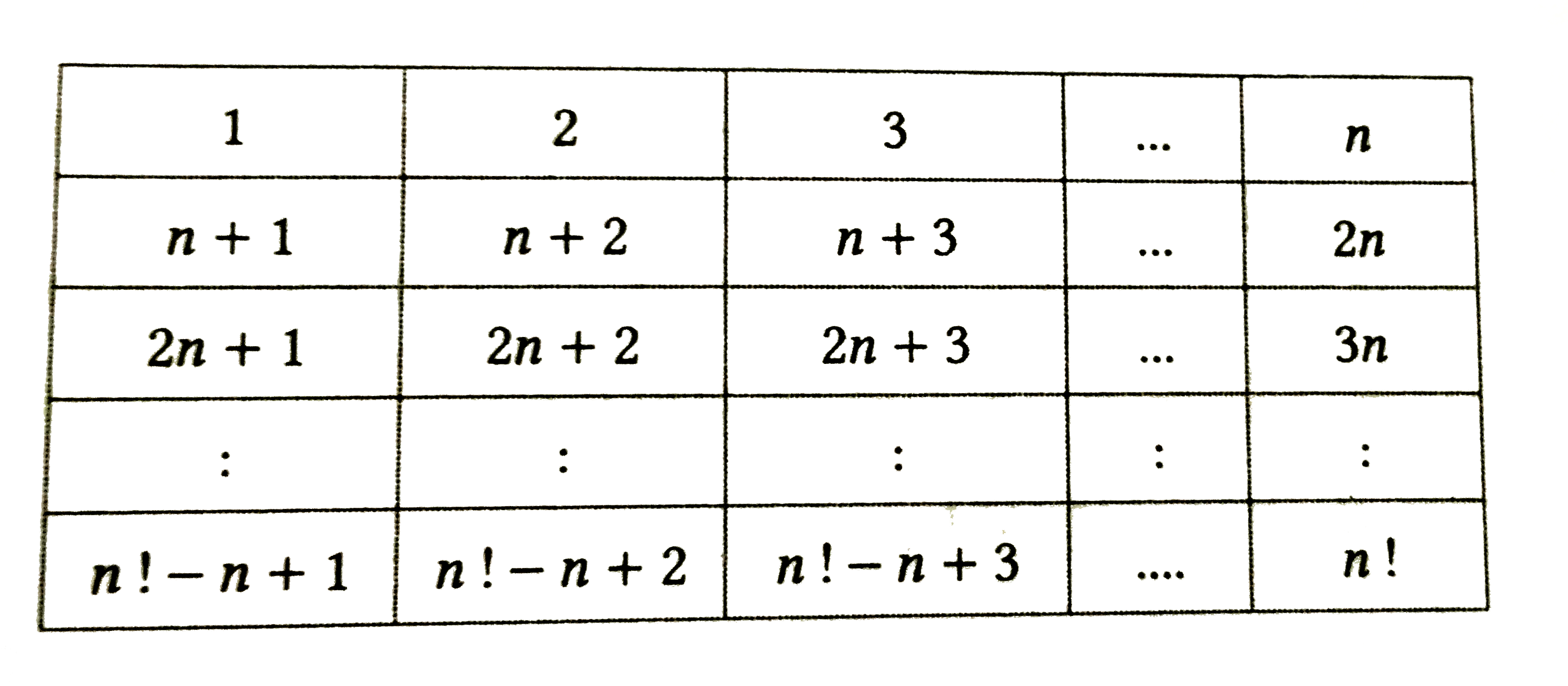 ltBrgt Each of these (n-1)! rows contains n consecutive positive integers. the products of the conescutive integers in each row is divisible by n!. thus, the product of all the integers from 1 to n! is divisible by `(n1)^((n-1)!)`.
ltBrgt Each of these (n-1)! rows contains n consecutive positive integers. the products of the conescutive integers in each row is divisible by n!. thus, the product of all the integers from 1 to n! is divisible by `(n1)^((n-1)!)`.