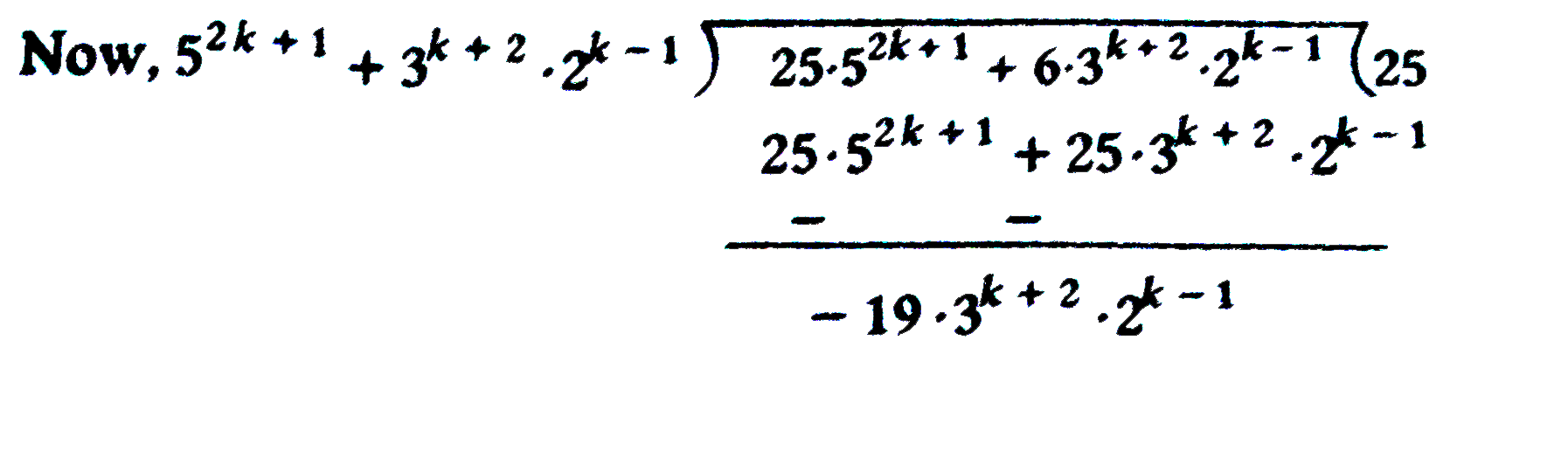Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Use the principle of mathematical induction to show that 5^(2n+1)+3^(n...
Text Solution
|
- Using the Principle of mathematical induction, show that 11^(n+2)+12^...
Text Solution
|
- Using principle of mathematical induction, prove that 7^(4^(n)) -1 is ...
Text Solution
|
- Show by using the principle of mathematical induction that for all nat...
Text Solution
|
- Using the principle of Mathematical Induction, show that 2.4^(2n+1)+3^...
Text Solution
|
- Prove by principle of Mathematical Induction that for all natural numb...
Text Solution
|
- Using principle of mathematical induction, prove that 7^(4^(n)) -1 is ...
Text Solution
|
- Prove the following by using the principle of mathematical induction f...
Text Solution
|
- Prove the statement by the principle of mathematical induction : 3^...
Text Solution
|