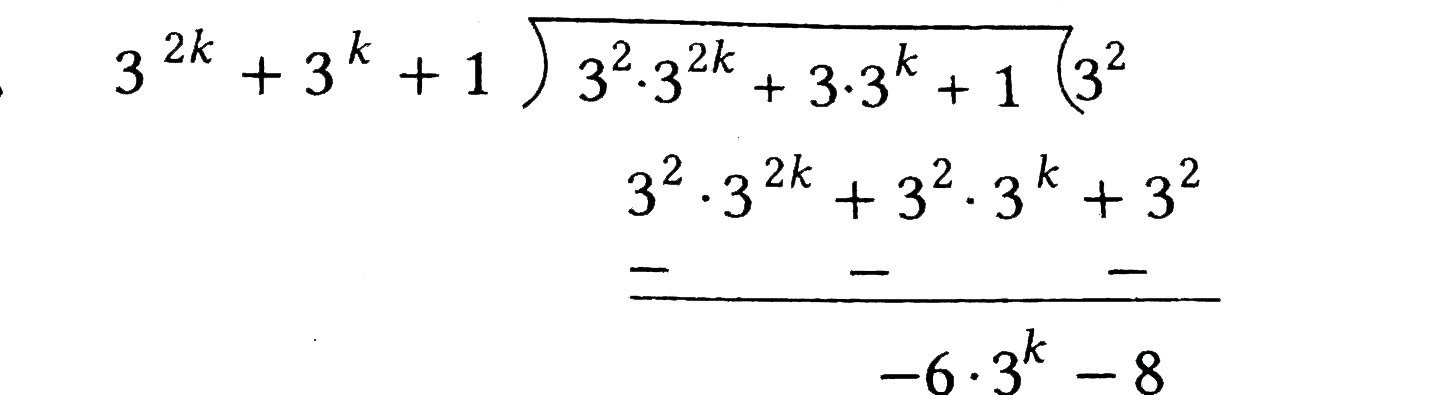Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Prove by induction that if n is a positive integer not divisible by 3,...
Text Solution
|
- Prove by induction that the sum Sn=n^3+2n^2+5n+3 is divisible by 3 for...
Text Solution
|
- For any positive integer n,prove that n^(3)-n is divisible by 6
Text Solution
|
- For any positive integer n , prove that n^3-n divisible by 6.
Text Solution
|
- यदि =n एक धनात्मक पूर्णांक हो तो सिद्ध कीजिये की 3^(2n+1)+2^(n+2),7 से...
Text Solution
|
- Prove by mathematical induction that for any positive integer n , 3^(2...
Text Solution
|
- For any positive integer n,3^(2n)+7 is divisible by 8 . Prove by mathe...
Text Solution
|
- For any positive integer n prove that n^(3)-n is divisible by 6
Text Solution
|
- ধনাত্মক পূর্ণসংখ্যা n -এর জন্য , n^3+2n সর্বদা বিভাজ্য হয়
Text Solution
|