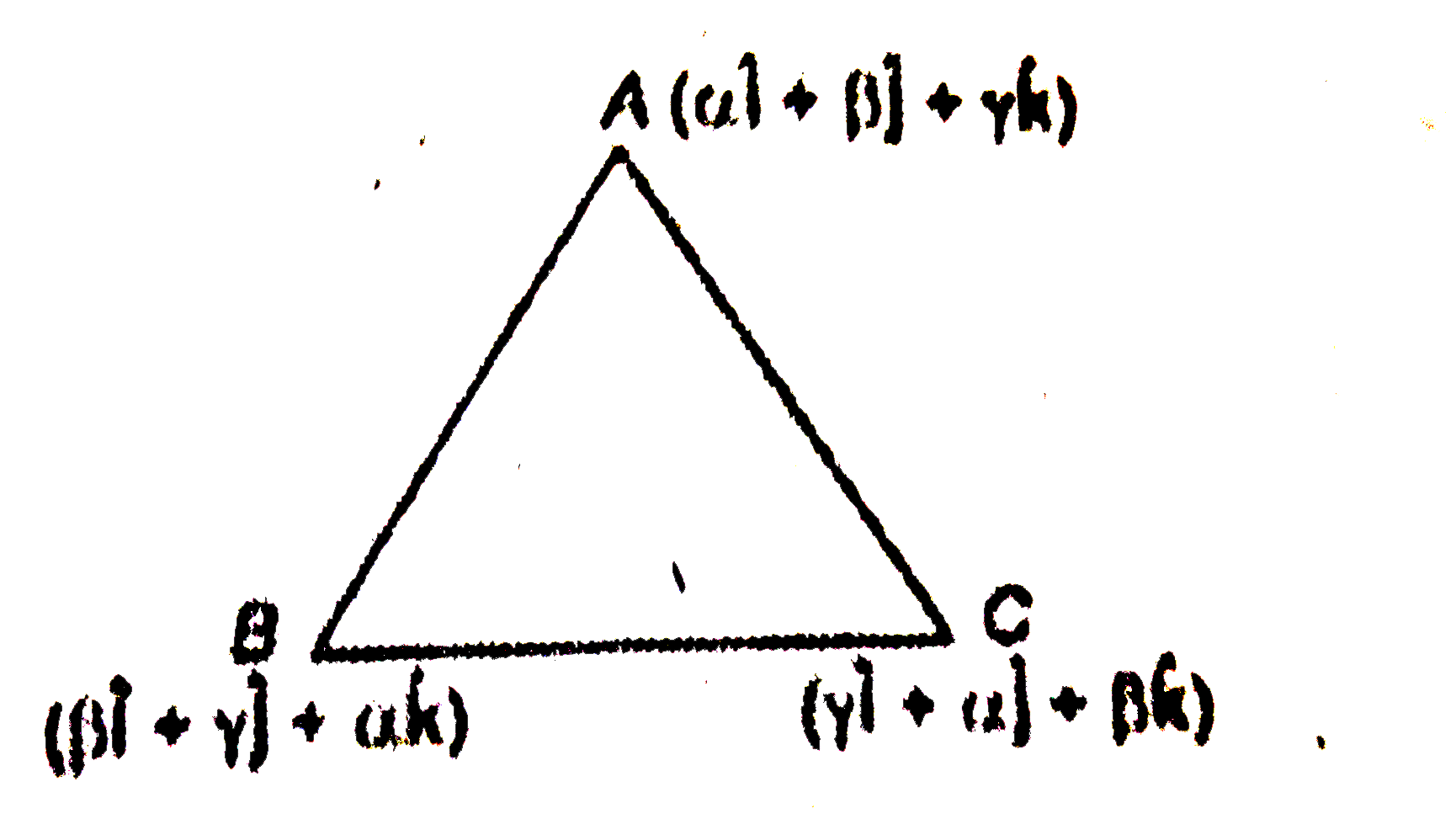A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let alpha, beta, gamma are distinct real numbers. The points with posi...
Text Solution
|
- Consider the vectors hat i+cos(beta-alpha) hat j+cos(gamma-alpha) hat...
Text Solution
|
- Let alpha, beta, gamma be distinct real numbers.The points with positi...
Text Solution
|
- Let alpha, beta, gamma be distinct real numbers. The points with posit...
Text Solution
|
- Consider the vectors hat i+cos(beta-alpha) hat j+cos(gamma-alpha) hat...
Text Solution
|
- Let alpha, beta and gamma be distinct real numbers. The points whose ...
Text Solution
|
- माना alpha,beta,gamma भिन्न वास्तविक संख्यायें हैं | बिन्दु जिनके स्थि...
Text Solution
|
- यदि सदिश i+j+k, सदिशों i, j, k के साथ क्रमश: alpha,beta,gamma कोण बनात...
Text Solution
|
- Let alpha, beta, gamma are distinct real numbers. The points with posi...
Text Solution
|