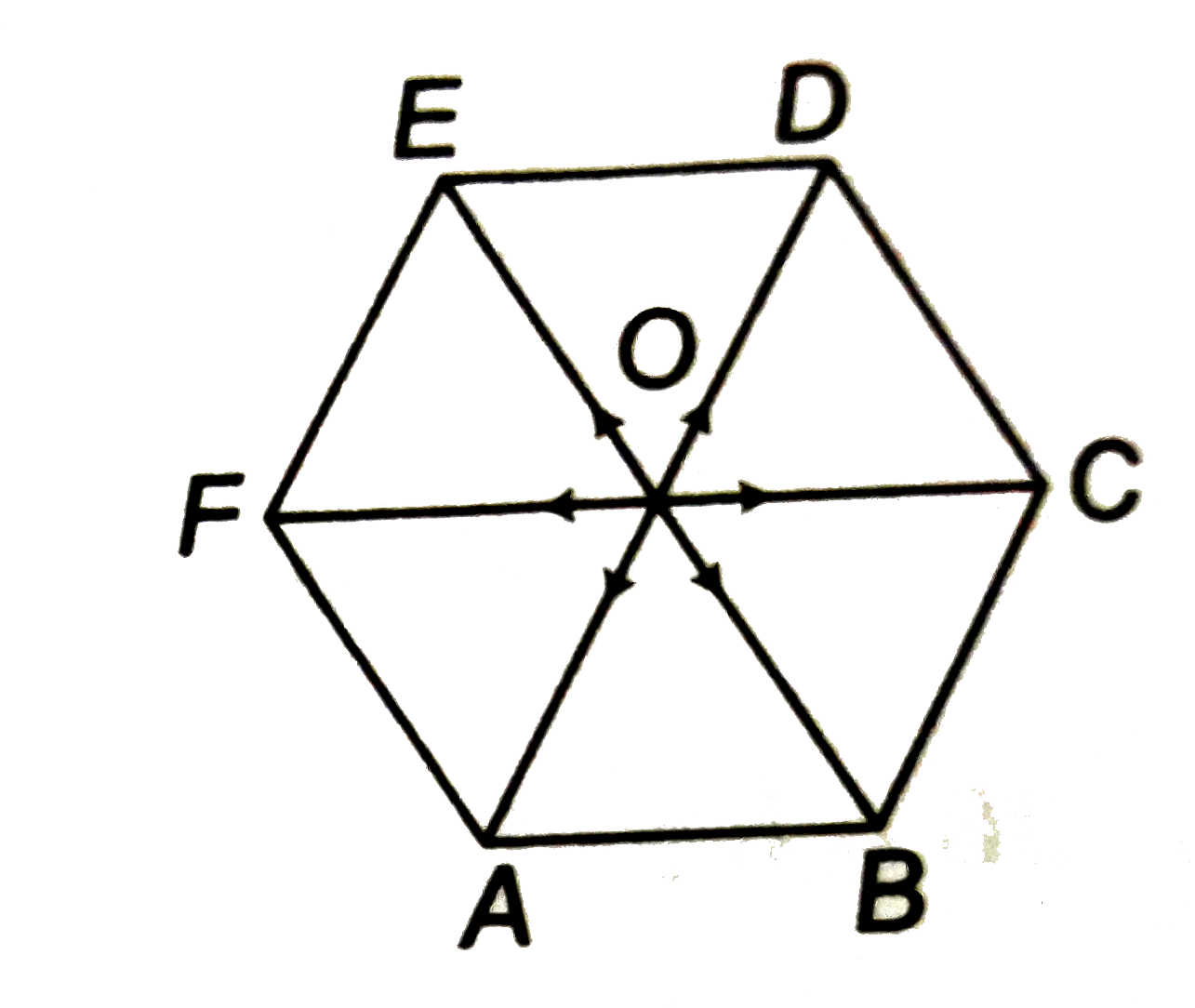A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a regular hexagon A B C D E F ,\ A vec B=a ,\ B vec C= vec b\ a n d...
Text Solution
|
- A B C D E is pentagon, prove that vec A B + vec B C + vec C D ...
Text Solution
|
- In a regular hexagon A B C D E F ,\ vec (AB)=a ,\ vec(B C)= vec b , ...
Text Solution
|
- If ABCDEF is a regular hexagon , then A vec D + E vec B + F vec C equ...
Text Solution
|
- ABCDEF si a regular hexagon with centre at the origin such that A vec...
Text Solution
|
- If ( vec axx vec b)xx( vec bxx vec c)= vec b ,w h e r e vec a , vec b ...
Text Solution
|
- A B C D E is pentagon, prove that vec A B + vec B C + vec C D ...
Text Solution
|
- A B C D E is pentagon, prove that vec A B + vec B C + vec C D ...
Text Solution
|
- A B C D E is pentagon, prove that vec A B + vec B C + vec C D +...
Text Solution
|