Home
Class 12
MATHS
In a parallelogram OABC, vectors vec a, ...

In a parallelogram `OABC,` vectors `vec a, vec b, vec c` are respectively the positions of vectors of vertices `A, B, C` with reference to O as origin. A point E is taken on the side BC which divide the line `2:1` internally. Also the line segment AE intersect the line bisecting the angle O internally in point P. If CP, when extended meets AB in point F. Then The position vector of point P, is

Text Solution

Verified by Experts

The correct Answer is:
B

let the position vector fo A and C be a and c respectively.
therefore,
Position vector of
`B=b=a+c` . . (i)
Also, position vector of
`E=(b+2c)/(3)=(a+3c)/(3)` . . . (ii)
Now, point P lies on angle bisector off `angleAOC`. thus,
Position vector of point
`P=lamda((a)/(|a|)+(b)/(|b|))` . . (iii)
Also, let P divides EA in ration `mu:1`. therefore, position vector of P
`=(mua+(a+3c)/(3))/(mu+1)=((3mu+1)a+3c)/(3(mu+1))` . . . (iv)
Comparing eqs. (iii) and (iv), we get
`lamda((a)/(|a|)+(c)/(|c|))=((3mu+1)a+3c)/(3(mu+1))`
`implies(lamda)/(|a|)=(3mu+1)/(3(mu+1)) and (lamda)/(|c|)=(1)/(mu+1)`
`implies(3|c|-|a|)/(3|a|)=mu`
`implies(lamda)/(|c|)=(1)/((3|c|-|a|)/(3|a|)+1)implies lamda=(3|a||c||)/(3|c|+2|a|)`
so, position vector off `P` is `(3|a||c|)/(3|c|+2|a|)((a)/(|a|)+(c)/(|c|))`.
Promotional Banner

Similar Questions

Explore conceptually related problems

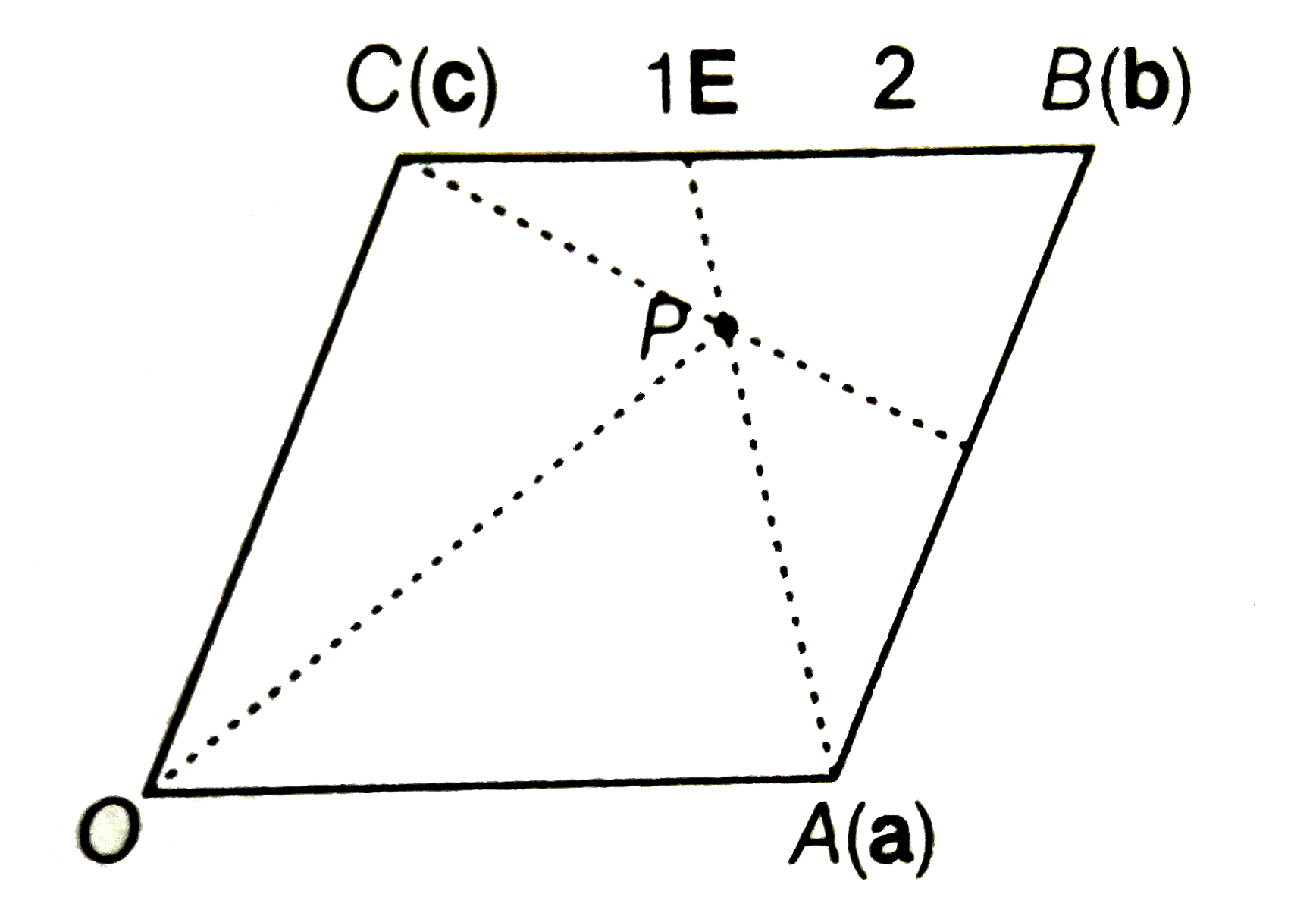
In a parallelogram OABC vectors a,b,c respectively, THE POSITION VECTORS OF VERTICES A,B,C with reference to O as origin. A point E is taken on the side BC which divides it in the ratio of 2:1 also, the line segment AE intersects the line bisecting the angle angleAOC internally at point P. if CP when extended meets AB in points F, then Q. The position vector of point P is

If vec a, vec b, vec c are mutually perpendicular unit vectors then |vec a + vec b + vec c| =

If a and b are position vector of two points A,B and C divides AB in ratio 2:1, then position vector of C is

If the position vector of a point A is vec a + 2 vec b and vec a divides AB in the ratio 2:3 , then the position vector of B, is

Let vec a, vec b and vec c be three vectors. Then scalar triple product [vec a, vec b, vec c]=

L and M are two points with position vectors 2vec(a) - vec(b) and vec(a) + 2vec(b) respectively. Write the position vectors of a point N which divides the line segment LM in the ratio 2 : 1 externally.

The position vector of the point which divides the join of points 2 vec a - 3 vec b and vec a + vec b in the ratio 3:1 is