Home
Class 12
MATHS
Let vec a , vec b and vec c be unit vec...

Let ` vec a , vec b` and `vec c` be unit vectors such that ` vec a+ vec b- vec c=0.` If the area of triangle formed by vectors ` vec a and vec b` is `A ,` then what is the value of `4A^2?`

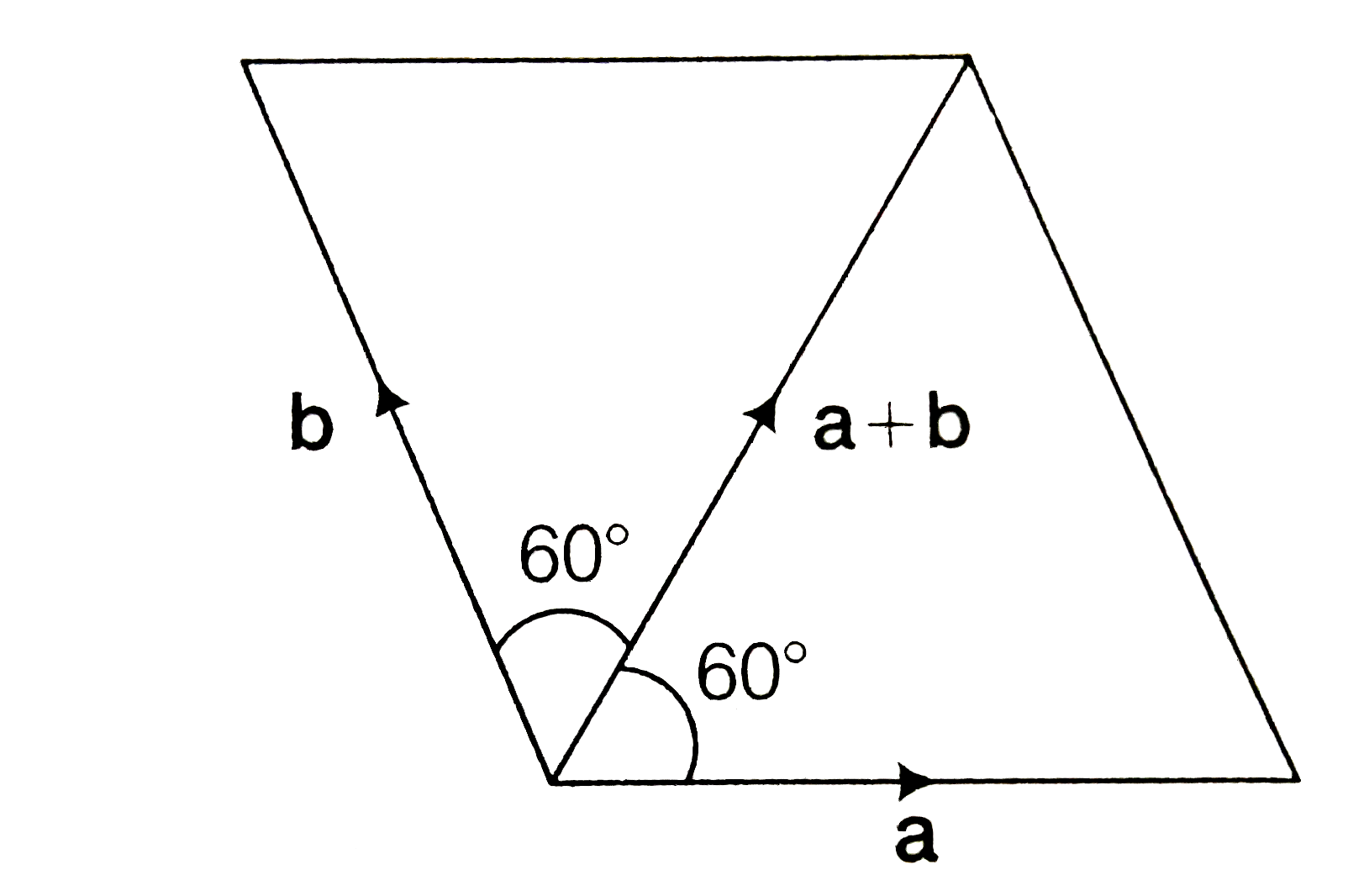
Text Solution

Verified by Experts

The correct Answer is:
3
Given a+b=c
Now, vector c is along the diagonal of the parallelogram which has adjacent side vectors a and b. sincne, c is also a unit vector, triangle formed by vectors a and b is an equilateral triangle.
Then, area of triangle `=(sqrt(3))/(4)impliesA^(2)=(3)/(10)implies16A^(2)=3`.
Promotional Banner

Similar Questions

Explore conceptually related problems

If vec a and vec b are unit vectors such that |vec a + vec b| =1, then |vec a - vec b| =

Let vec a, vec b, vec c be unit vectors such that vec a + vec b + vec c = vec 0 . Which one of the following is correct?

If vec a, vec b, vec c are unit vectors such that vec a + vec b + vec c = vec 0 , then the value of vec a . vec b + vec b.vec c + vec c vec a is equal to

Let vec a, vec b and vec c be three vectors. Then scalar triple product [vec a, vec b, vec c]=

If vec a and vec b are unit vectors such that |vec a xx vec b| = vec a . vec b , then |vec a + vec b|^(2) =

If vec a, vec b and vec c are non coplanar unit vectors such that vec a xx (vec b xx vec c) = (vec b + vec c)/sqrt2 , then

If vec a and vec b are vectors such that |vec a + vec b| = |vec a - vec b| , then the angle between vec a and vec b is