A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
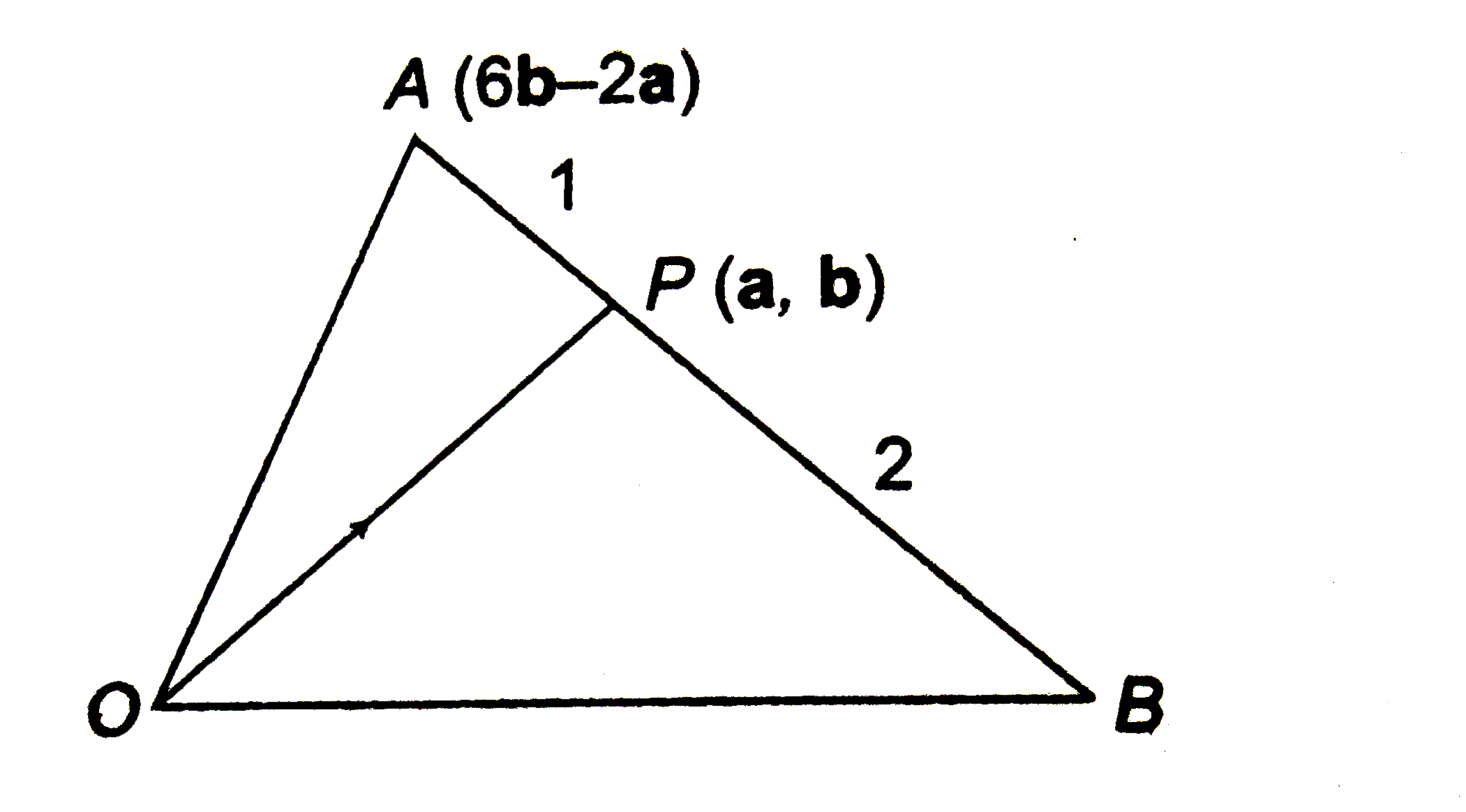
- A and B are two points. The position vector of A is 6b-2a. A point P ...
Text Solution
|
- If the position vector of a point A is vec a + 2 vec b and vec a divi...
Text Solution
|
- एक बिन्दु P का मान a + 2b है। यदि P का मान a है तथा P, AB को 2 : 3 के ...
Text Solution
|
- यदि बिंदु A का स्थिति सदिश ( vec (a ) + 2 vec (b )) और बिंदु ...
Text Solution
|
- If a and b are position vector of two points A,B and C divides AB in r...
Text Solution
|
- The position vector of a point A is veca+2vecb and veca divides AB i...
Text Solution
|
- bara,barb are position vectors of points A and B. If P divides AB in t...
Text Solution
|
- A और B दो बिंदु है। बिंदु B का स्थिति सदिश vec(a) + 2vec(b) है। बि...
Text Solution
|
- A एवं B दो बिन्दु हैं | A का स्थिति सदिश 6b-2a है | एक बिन्दु P, रेखा ...
Text Solution
|