Home
Class 12
MATHS
In a regular hexagon ABCDEF, prove that ...

In a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.

A

2

B

3

C

4

D

6

Text Solution

Verified by Experts

The correct Answer is:
B
By triangle law, `AB=AD-BD,AC=AD-CD`

Therefore, `AB+AC+AD+AE+AF`
`=3AD+(AE-BD)+(AF-CD)=3AD`
hence, `lamda=3" "(becauseAE=BD,AF=CD)`
Promotional Banner

Similar Questions

Explore conceptually related problems

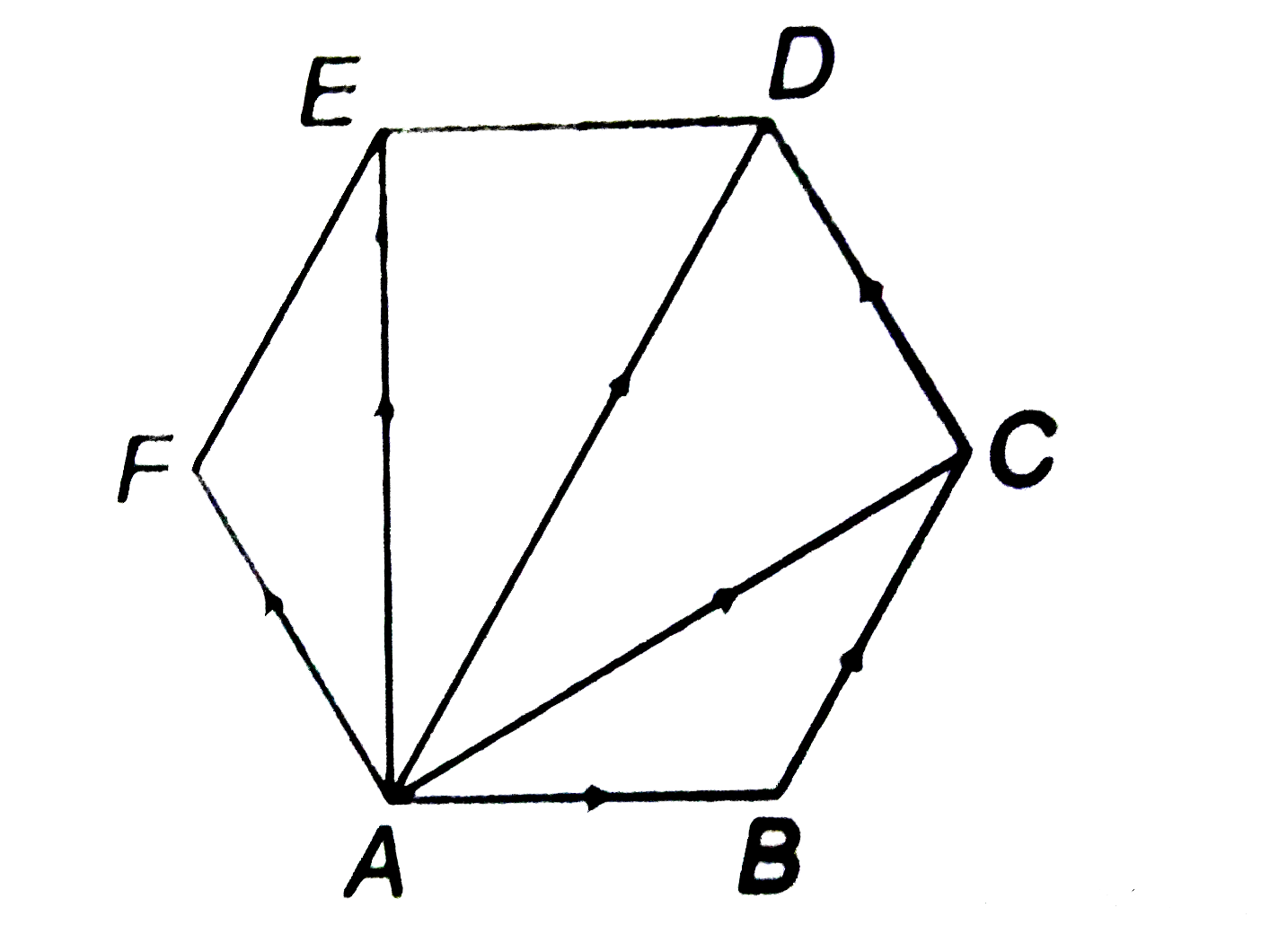
In a regular hexagon ABCDEF, bar(AB) + bar(AC)+bar(AD)+ bar(AE) + bar(AF)=k bar(AD) then k is equal to

Consider the regular hexagon ABCDEF with centre at O (origin). Q. Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant is (a)3AO (b)2AO (c)4AO (d)6AO

If ABCDEF is a regular hexagon then vec AD + vec EB + vec FC =

In the given figure , BD bot AC .Prove that AB^2 +CD^2 = AD^2 +BC^2

A uniform wire of resistance 24 Omega is bent in form of a regular hexagon ABCDEF . A cell of e.m.f. 4 volt having negligible internal resistance is connected across the side AB of the hexagon. The field at its centre will be

In an equilateral triangle ABC, AD _|_ BC . Prove that : AB^(2) + CD^(2) = 5/4 AC^(2)

In Fig . AD is a median of a triangle ABD and AM bot BC. Prove that : AC^(2)=AD^(2)+BC. DM+((BC)/(2))^(2)

In the Fig. AD and BE are medians of DeltaABC and BE"||"DF . Prove that CF=(1)(4)AC.

A quadrilateral ABCD is drawn to circumscribe a circle as shown. Prove that AB+CD=AD +BC.